Beats - Analytical method and Uses of beats

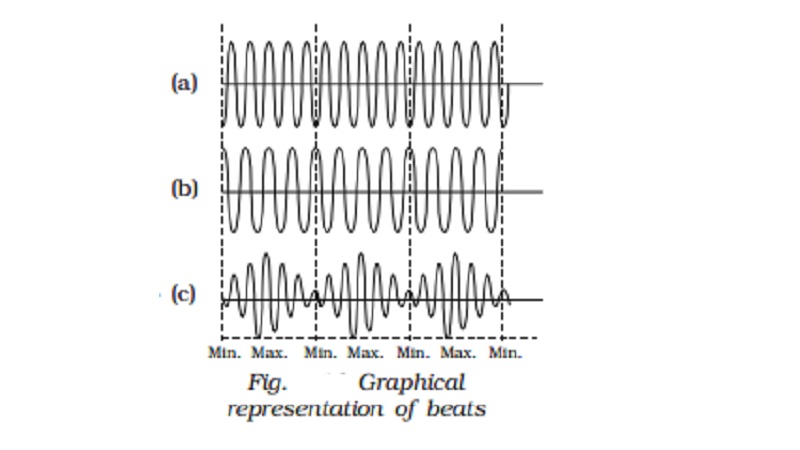
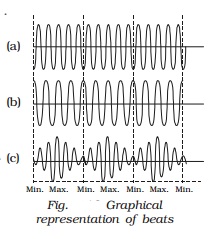
Beats

When two waves of nearly equal frequencies travelling in a medium along the same direction superimpose upon each other, beats are produced. The amptitude of the resultant sound at a point rises and falls regularly.

The intensity of the resultant sound at a point rises and falls regularly with time. When the intensity rises to maximum we call it as waxing of sound, when it falls to minimum we call it as waning of sound.

The phenomenon of waxing and waning of sound due to interference of two sound waves of nearly equal frequencies are called beats. The number of beats produced per second is called beat frequency, which is equal to the difference in frequencies of two waves.

Analytical method

Let us consider two waves of slightly different frequencies n₁ and n₂ (n₁ ~ n₂ < 10) having equal amplitude travelling in a medium in the same direction.

At time t = 0, both waves travel in same phase. The equations of the two waves are

y₁ = a sin ω₁t

y₁ = a sin (2π n1)t ...(1)

y₂ = a sin ω₂ t = a sin (2π n₂)t ...(2)

When the two waves superimpose, the resultant displacement is given by

y = y₁ + y₂

y = a sin (2π n₁) t + a sin (2π n₂) t           ???(3)

Therefore

y = 2a sin 2π (n₁+n₂ / 2)t. cos 2π(n₁-n₂ / 2)t  ??(4)

Substitute A = 2 a cos 2π(n₁-n₂ / 2)

And

n=(n₁+n₂)/ 2 in equation (4)

∴ y = A sin 2πnt

This represents a simple harmonic wave of frequency n = (n₁+n₂ / 2) and amplitude A which changes with time.

(i) The resultant amplitude is maximum (i.e) ? 2a, if

cos 2π[( n₁-n₂ )/ 2]t=? 1

2π[( n₁-n₂ )/ 2]t = m π

where m = 0, 1, 2 ...) or (n₁ ? n₂) t = m

The first maximum is obtained at t₁ = 0

The second maximum is obtained at

t₂ = 1/(n₁-n₂)

The third maximum at t₃ = 2/(n₁-n₂) and so on.

The time interval between two successive maxima is

t₂ ? t₁ = t₃ ? t₂ = 1/(n₁-n₂)

Hence the number of beats produced per second is equal to the reciprocal of the time interval between two successive maxima.

(ii) The resultant amplitude is minimum (i.e) equal to zero, if

cos 2π ( (n₁-n₂) /2)t=0

(i.e) 2π ( (n₁-n₂) /2)t= π/2 + m π

where m = 0, 1, 2 ...

The first minimum is obtained at

t₁′ = 1 /[2(n₁-n₂)]

The second minimum is obtained at

t₂′ = 3 /[2(n₁-n₂)]

The third minimum is obtained at

t₃′ = 5 /[2(n₁-n₂)] and so on

Time interval between two successive minima is

t₂′ - t₁′ = t₃′ ? t₂′ = 1/ (n₁-n₂)

Hence, the number of beats produced per second is equal to the reciprocal of time interval between two successive minima.

Uses of beats

(i)  The phenomenon of beats is useful in tuning two vibrating bodies in unison. For example, a sonometer wire can be tuned in unison with a tuning fork by observing the beats. When an excited tuning fork is kept on the sonometer and if the sonometer wire is also excited, beats are heard, when the frequencies are nearly equal. If the length of the wire is adjusted carefully so that the number of beats gradually decreases to zero, then the two are said to be in unison. Most of the musical instruments are made to be in unison based on this method.

The frequency of a tuning fork can be found using beats. A standard tuning fork of frequency N is excited along with the experimental fork. If the number of beats per second is n, then the frequency of experimental tuning fork is N+n. The experimental tuning fork is then loaded with a little bees? wax, thereby decreasing its frequency. Now the observations are repeated. If the number of beats increases, then the frequency of the experimental tuning fork is N-n, and if the number of beats decreases its frequency is N + n.