Basic logic gates using discrete components

Logic gates

Circuits which are used to process digital signals are called logic gates. They are binary in nature. Gate is a digital circuit with one or more inputs but with only one output. The output appears only for certain combination of input logic levels. Logic gates are the basic building blocks from which most of the digital systems are built up. The numbers 0 and 1 represent the two possible states of a logic circuit. The two states can also be referred to as 'ON and OFF' or 'HIGH and LOW' or 'TRUE and FALSE'.

Basic logic gates using discrete components

The basic elements that make up a digital system are 'OR', 'AND' and 'NOT' gates. These three gates are called basic logic gates. All the possible inputs and outputs of a logic circuit are represented in a table called TRUTH TABLE. The function of the basic gates are explained below with circuits and truth tables.

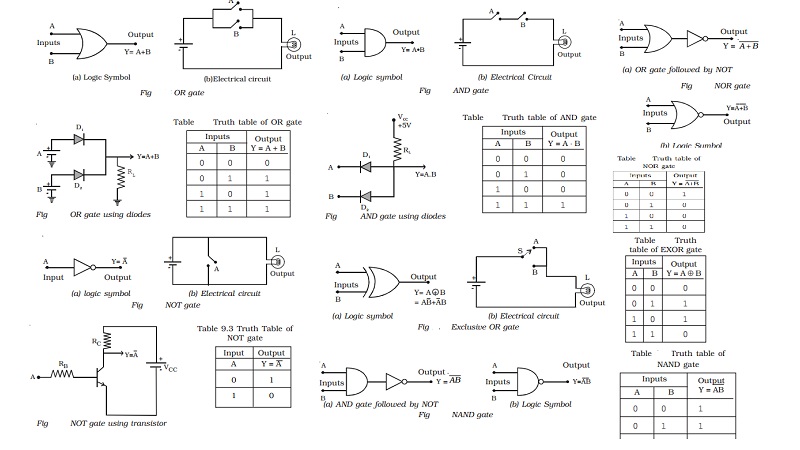
(i) OR gate

An OR gate has two or more inputs but only one output. It is known as OR gate, because the output is high if any one or all of the inputs are high. The logic symbol of a two input OR gate is shown in Fig a.

The Boolean expression to represent OR gate is given by Y= A+B (+ symbol should be read as OR)

The OR gate can be thought of like an electrical circuit shown in Fig b, in which switches are connected in parallel with each other. The lamp will glow if both the inputs are closed or any one of them is closed.

Diode OR gate

Fig shows a simple circuit using diodes to build a two input OR gate. The working of this circuit can be explained as follows.

Case (i) A = 0 and B = 0

When both A and B are at zero level, (i.e.) low, the output voltage will be low, because the diodes are non-conducting.

Case (ii) A = 0 and B = 1

When A is low and B is high, diode D₂ is forward biased so that current flows through R_L and output is high.

Case (iii) A = 1 and B = 0

When A is high and B is low, diode D₁ conducts and the output is high.

Case (iv) A = 1 and B = 1

When A and B both are high, both diodes D₁ and D₂ are conducting and the output is high. Therefore Y is high. The OR gate operations are shown in Table

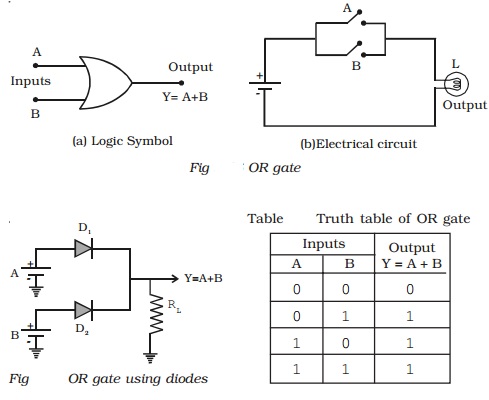
(ii) AND gate

An AND gate has two or more inputs but only one output. It is known as AND gate because the output is high only when all the inputs are high. The logic symbol of a two input AND gate is shown in Fig a.

Y = A⋅B ( ⋅ should be read as AND)

AND gate may be thought of an electrical circuit as shown in Fig b, in which the switches are connected in series. Only if A and B are closed, the lamp will glow, and the output is high.

Diode AND gate

Fig  shows a simple circuit using diodes to build a two-input AND gate. The working of the circuit can be explained as follows :

Case (i) A = 0 and B = 0

When A and B are zero, both diodes are in forward bias condition and they conduct and hence the output will be zero, because the supply voltage V_CC will be dropped across R_L only. Therefore Y = 0.

Case (ii) A = 0 and B = 1

When A = 0 and B is high, diode D₁ is forward biased and diode D₂ is reverse biased. The diode D₁ will now conduct due to forward biasing. Therefore, output Y = 0.

Case (iii) A = 1 and B = 0

In this case, diode D₂ will be conducting and hence the output Y = 0.

Case (iv) A = 1 and B = 1

In this case, both the diodes are not conducting. Since D₁ and D₂ are in OFF condition, no current flows through R_L. The output is equal to the supply voltage. Therefore Y = 1.

Thus the output will be high only when the inputs A and B are high. The Table 9.2 summarises the function of an AND gate.

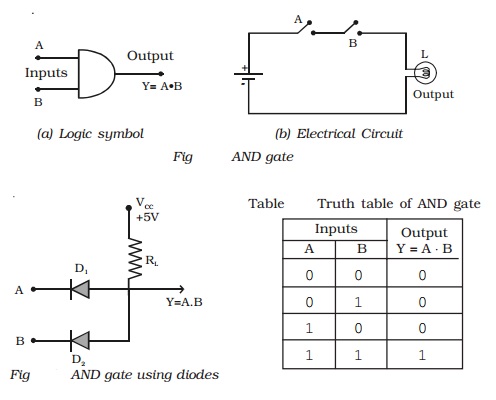
(iii) NOT gate (Inverter)

The NOT gate is a gate with only one input and one output. It is so called, because its output is complement to the input. It is also known as inverter. Fig a shows the logic symbol for NOT gate.

The Boolean expression to represent NOT operation is Y =  A .

The NOT gate can be thought of like an electrical circuit as shown in Fig b. When switch A is closed, input is high and the bulb will not glow (i.e) the output is low and vice versa.

Fig  is a transistor in CE mode, which is used as NOT gate. When the input A is high, the transistor is driven into saturation and hence the output Y is low. If A is low, the transistor is in cutoff and hence the output Y is high. Hence, it is seen that whenever input is high, the output is low and vice versa. The operation of NOT gate is shown in Table 9.3.

Exclusive OR gate (EXOR gate)

The logic symbol for exclusive OR (EXOR) gate is shown in

The Boolean expression to represent EXOR operation is

Y = A ⊕ B

EXOR gate has an output 1, only when the inputs are complement to each other.

The equivalent switching circuit is shown in Fig b.

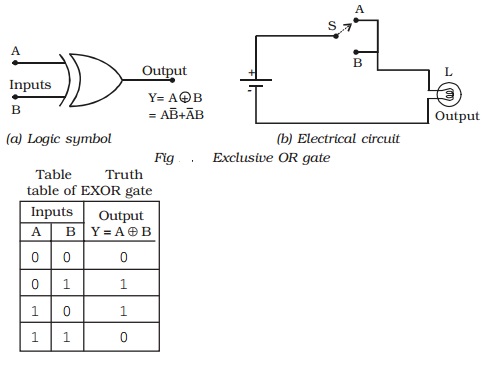
Switch positions A and B will individually make the lamp to be ON. But the combination of A and B is not possible.

The EXOR operation is represented in Table.

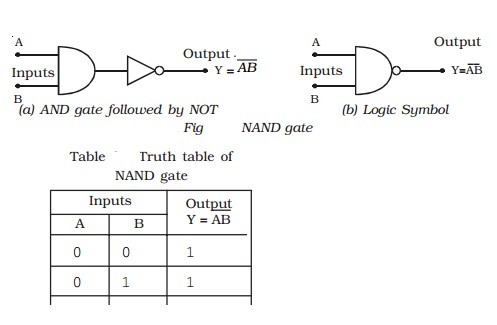
NAND gate

This is a NOT-AND gate. It can be obtained by connecting a NOT gate at the output of an AND gate (Fig a).

The logic symbol for NAND gate is shown in Fig b.

NAND gate function is reverse of AND gate function. A NAND gate will have an output,

only if both inputs are not 1. In other words, it gives an output 1, if either A or B or both are 0. The

operation of a NAND gate is represented in Table.

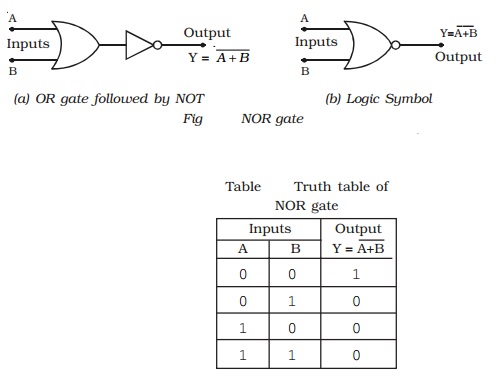
NOR gate

This is a NOT-OR gate. It can be made out of an OR gate by connecting an inverter at its output (Fig a).

The logic symbol for NOR gate is given in Fig b

The NOR gate function is the reverse of OR gate function. A NOR gate will have an output, only when all inputs are 0. In a NOR gate, output is high, only when all inputs are low. The NOR operation is represented in Table.