Relation between the three moduli of elasticity

Relation between the three moduli of elasticity

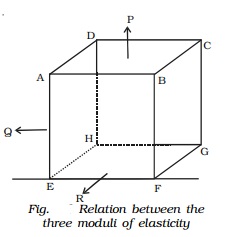
Suppose three stresses P, Q and R act perpendicular to the three facesABCD, ADHE and ABFE of a cube of unit volume (Fig.). Each of these stresses will produce an extension in its own direction and a compression along the other two perpendicular directions. If λ is the extension per unit stress, then the elongation along the direction of P will be λP. If µ is the contraction per unit stress, then the contraction along the direction of P due to the other two stresses will be µQ and µR.

The net change in dimension along the direction of P due to all the stresses is e = λP - µQ - µR.

Similarly the net change in dimension along the direction of Q is f = λQ - µP - µR and the net change in dimension along the direction of R is g = λR - µP - µQ.

Case (i)

If only P acts and Q = R = 0 then it is a case of longitudinal stress.

∴ Linear strain = e = λP

Young's modulus q =linear stress /linear strain = P / λP

q= 1/λ

 or

 λ = 1/q       ……………....(1)

Case (ii)

If R = O and P = - Q, then the change in dimension along P is e = λP - µ (-P)

(i.e) e = (λ + µ) P

Angle of shear θ = 2e* = 2 (λ + µ) P

Rigidity modulus

n = P/θ

 = P/ 2(λ+ µ)P   ……………..(2)

Case (iii)

If P = Q = R, the increase in volume is = e + f + g

= 3 e = 3 (λ − 2µ) P (since e = f = g)

∴ Bulk strain = 3(λ−2µ) P

Bulk modulus k = P / 3(λ - 2µ)P

Or   (λ − 2µ)= 1/3k            ……………(3)

From (2), 2(λ + µ) = 1/n

2λ + 2µ = 1/n

From (3), (λ − 2µ) = 1/3k

Adding (4) and (5)

3λ = 1/n + 1/3k

λ = 1/3n + 1/9k

∴ From (1),

1/q = 1/3n + 1/9k

9/q = 3/n + 1/k

This is the relation between the three moduli of elasticity.