Chapter: 11th 12th std standard Class Physics sciense Higher secondary school College Notes
Three moduli of elasticity
Three moduli of elasticity
Depending upon the type of strain in the body
there are three different types of modulus of elasticity. They are
(i)
Young's modulus
(ii)
Bulk modulus
(iii)
Rigidity modulus
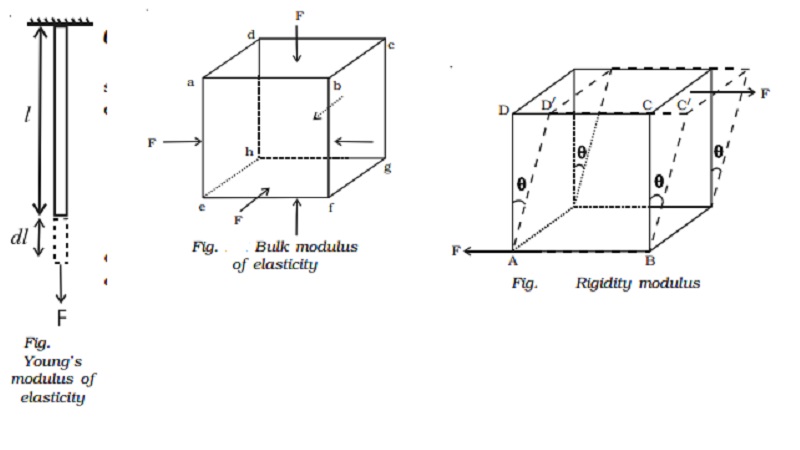
(i) Young's modulus of elasticity
Consider a wire of length l
and cross sectional area A stretched by a force F acting along its length. Let
dl be the extension produced.
Longitudinal stress = Force / Area = F/A
Longitudinal strain = change
in length / original length = dl/l
Young's modulus of the
material of the wire is defined as the ratio of longitudinal stress to
longitudinal strain. It is denoted by q.
Young's modulus =
longitudinal stress / longitudinal strain
q =F/A / dl/l = Fl /Adl
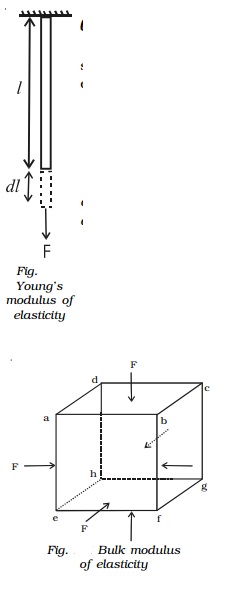
(ii) Bulk modulus of elasticity
Suppose euqal forces act
perpendicular to the six faces of a cube of volume V as shown in Fig.. Due
to the action of these
forces, let the decrease in volume be dV.
Now, Bulk stress = Force/Are
= F/ A
Bulk Strain = change in volume / original volume = -dV/V
(The negative sign indicates
that volume decreases.)
Bulk modulus of the material
of the object is defined as the ratiobulk stress to bulk strain.
It is denoted by k
Bulk modulus = Bulk stress / Bulk strain
K = -PV/dV
(iii) Rigidity modulus or shear modulus
Let us apply a force
Ftangential to the top surface of a block whose bottom AB is fixed, as shown in
Fig..
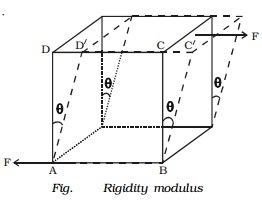
Under the action of this
tangential force, the body suffers a slight change in shape, itsvolume
remaining unchanged.The side AD of the block is sheared through an angle θ to
the position AD'.
If the area of the top
surface is A, then shear stress = F/A.
Shear modulus or rigidity
modulus of the material of the object isdefined as the ratio of shear stress to
shear strain. It is denoted by n.
Rigidity modulus = shear
stress / shear strain
(i.e) n = F/Aθ
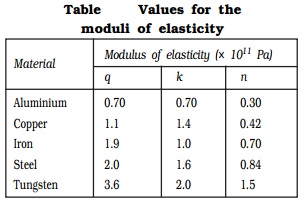
Table lists the values of the three moduli of
elasticity for some commonly used materials.
Related Topics