Motion on a level circular road

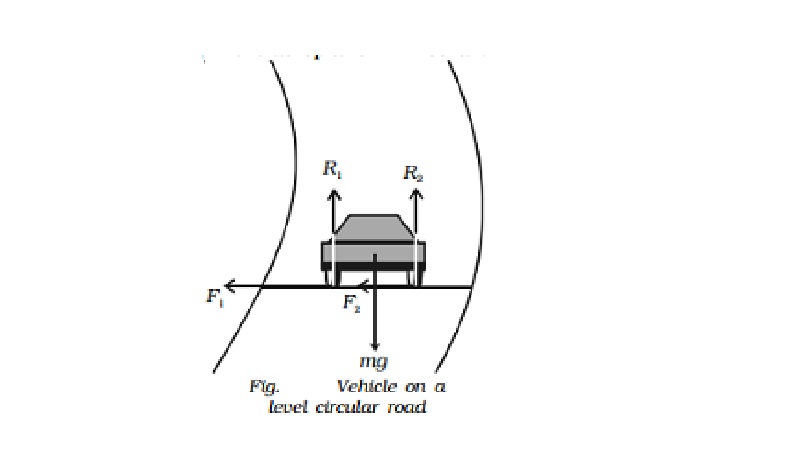
Motion on a level circular road

When a vehicle goes round a level curved path, it should be acted upon by a centripetal force. While negotiating the curved path, the wheels of the car have a tendency to leave the curved path and regain the straight-line path. Frictional force between the tyres and the road opposes this tendency of the wheels. This frictional force, therefore, acts towards the centre of the circular path and provides the necessary centripetal force.

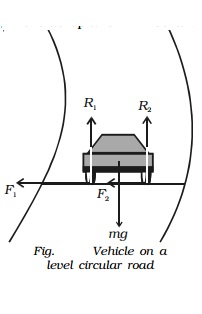
In Fig., weight of the vehicle mg acts vertically downwards. R1, R2 are the forces of normal reaction of the road on the wheels. As the road is level (horizontal), R1, R2 act vertically upwards. Obviously,

R1 + R2 = mg ...(1)

Let m * be the coefficient of friction between the tyres and the road, F1 and F2 be the forces of friction between the tyres and the road, directed towards the centre of the curved path.

∴ F1 = mR1 and F2 = mR2 ...(2)

If v is velocity of the vehicle while negotiating the curve, the centripetal force required = mv2/r .

As this force is provided only by the force of friction.

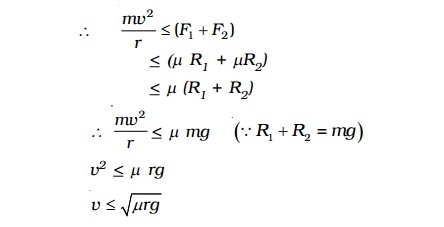
Hence the maximum velocity with which a car can go round a level curve without skidding is v = Ã-(mrg) . The value of v depends on radius r of the curve and coefficient of friction m between the tyres and the road.