Chapter: 11th 12th std standard Class Physics sciense Higher secondary school College Notes
Determination of coefficient of viscosity of water by Poiseuille's flow method
Poiseuille's equation
Poiseuille investigated the steady flow of a
liquid through a capillary tube. He derived an expression for the volume of the
liquid flowing per second through the tube.
Consider a liquid of co-efficient of viscosity η flowing, steadily through a horizontal capillary tube of length l and radius r. If P is the pressure
difference across the ends of the tube, then the volume V of the liquid flowing per second through the tube depends on η, r and the pressure
gradient p/l.
(i.e) V α ηx r y (P /l)z
V=k ηx r y (P /l)z
where k is a constant of proportionality.
Rewriting equation (1) in terms of dimensions,
[L3T-1] = [ML-1 T-1]
x [L]y[ML-1T-2 / L]z
Equating the powers of L, M and T on both sides we get x = -1, y =
4 and z = 1
Substituting in equation (1),
V= kPr4/ ηl
Experimentally k was found to
be equal to π/ 8
V = πPr4 / 8 ηl
This is known as Poiseuille's
equation.
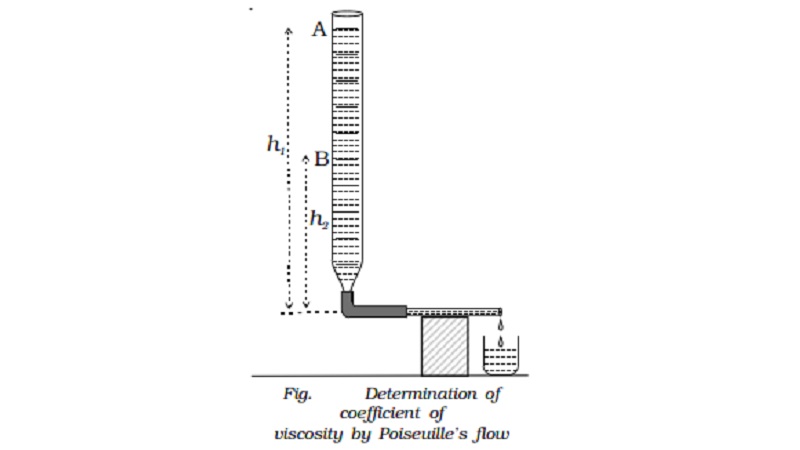
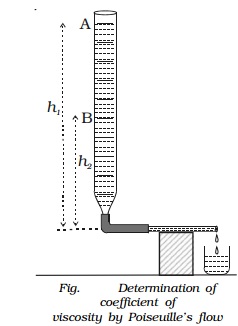
Determination of coefficient of viscosity of water by Poiseuille's
flow method
A capillary tube of very fine
bore is connected by means of a rubber tube to a burette kept vertically. The
capillary tube is kept horizontal as shown in Fig.. The burette is filled with
water and the pinch - stopper is removed. The time taken for water level to
fall from A to B is noted. If V is the volume between the two levels A and B,
then volume of liquid flowing per second is V/t. If l and r are the length and
radius of the capillary tube respectively, then
V/t = πPr4 / 8 η
 l
l
If ρ is the density of the liquid then the initial pressure
difference between the ends of the tube is P1 = h1ρg and
the final pressure difference P2 = h2ρg. Therefore the
average pressure difference during the flow of water is P where
P = (P1 + P2 ) /2
=[(h1+h2) /2 ]hg
Substituting in equation (1), we get
V/t = πhρgr4 /
8lη
or
η= πhρgr4t / 8lV
Viscosity - Practical applications
The importance of viscosity can be understood
from the following examples.
(i)
The knowledge of coefficient of viscosity of
organic liquids is used to determine their molecular weights.
(ii)
The knowledge of coefficient of viscosity and
its variation with temperature helps us to choose a suitable lubricant for
specific machines. In light machinery thin oils (example, lubricant oil used in
clocks) with low viscosity is used. In heavy machinery, highly viscous oils
(example, grease) are used.
Related Topics