Definition, Formula, Solved Example Problems - de Moivre's Theorem | 12th Mathematics : UNIT 2 : Complex Numbers
Chapter: 12th Mathematics : UNIT 2 : Complex Numbers
de Moivre's Theorem
de Moivre's Theorem
de MoivreŌĆÖs Theorem
Given any complex number cos╬Ė + i sin╬Ė and any integer n,
(cos╬Ė + i sin╬Ė )n = cos n╬Ė + i sin n╬Ė .
Corollary
(1) (cos╬Ė - i sin╬Ė )n = cos n╬Ė - i sin n╬Ė
(2) (cos╬Ė + i sin╬Ė )-n = cos n╬Ė - i sin n╬Ė
(3) (cos╬Ė - i sin╬Ė )-n = cos n╬Ė + i sin n╬Ė
(4) sin╬Ė + i cos╬Ė = i (cos╬Ė - i sin╬Ė ) .
Now let us apply de MoivreŌĆÖs theorem to simplify complex numbers and to find solution of equations.
Example 2.28
If z = (cos╬Ė + i sin╬Ė ) , show that zn + 1/ zn = 2 cos n╬Ė and zn ŌĆō [1/ zn] = 2i sin n╬Ė .
Solution
Let z = (cos╬Ė + i sin╬Ė ) .
By de MoivreŌĆÖs theorem ,
zn = (cos╬Ė + i sin╬Ė )n = cos n╬Ė + i sin n╬Ė
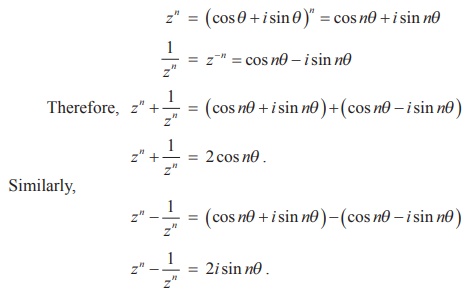
Example 2.29
Similarly, 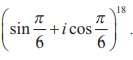
Solution
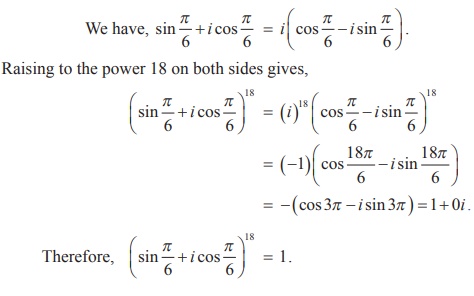
Example 2.30
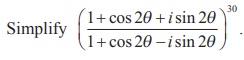
Solution
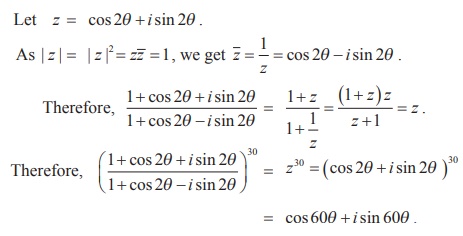
Example 2.31
Simplify
(i) (1+ i)18
(ii) (-ŌłÜ3 + 3i)31 .
Solution
(i) (1+ i)18
Let 1+ i = r (cos╬Ė + i sin╬Ė ) . Then, we get

(ii) (-ŌłÜ3 + 3i)31 .
Let -ŌłÜ3 + 3i = r (cos╬Ė + i sin╬Ė ) . Then, we get
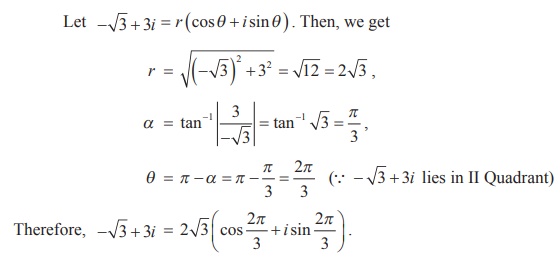
Raising power 31 on both sides,
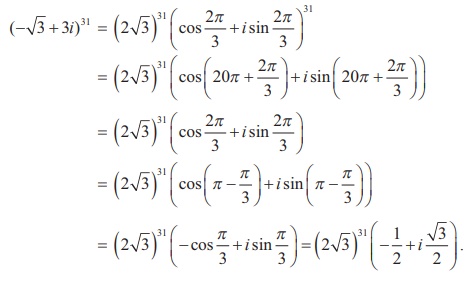
Related Topics