Problem Questions with Answer, Solution - Exercise 2.7: Polar and Euler form of a Complex Number | 12th Mathematics : UNIT 2 : Complex Numbers
Chapter: 12th Mathematics : UNIT 2 : Complex Numbers
Exercise 2.7: Polar and Euler form of a Complex Number
EXERCISE 2.7
1. Write in polar form of the following complex numbers
(i) 2 + i2ŌłÜ3
(ii) 3 - iŌłÜ3
(iii) -2 - i2
(iv) i -1 / [cos (ŽĆ/3) + i sin (ŽĆ/3)].



2. Find the rectangular form of the complex numbers
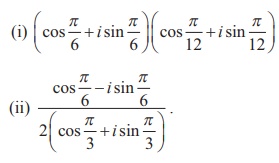

3. If ( x1 + iy1 )( x2 + iy2 )( x3 + iy3 )... ...( xn + iyn ) = a + ib , show that
(i) (x12 + y12 )(x22 + y22 )(x32 + y32 )... ...(xn2 + y n2 ) = a2 + b2
(ii) 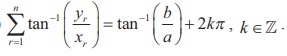

4. If 1+ z / 1- z = cos 2╬Ė + i sin 2╬Ė , show that z = i tan╬Ė .

5. If cos ╬▒ + cos ╬▓ + cos ╬│ = sin ╬▒ + sin ╬▓ + sin ╬│ = 0, show that
(i) cos 3╬▒ + cos 3╬▓ + cos 3╬│ = 3cos(╬▒ + ╬▓ + ╬│ ) and
(ii) sin 3╬▒ + sin 3╬▓ + sin 3╬│ = 3sin (╬▒ + ╬▓ + ╬│ ) .

6. If z = x + iy and arg ( z-i / z+2) = ŽĆ/4 , show that x2 + y2 + 3x - 3y + 2 = 0 .
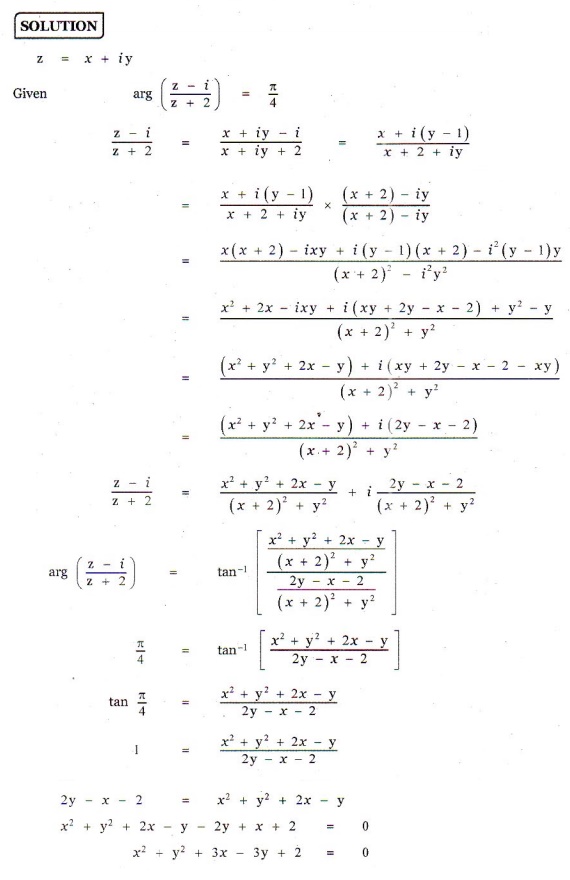
Answers:
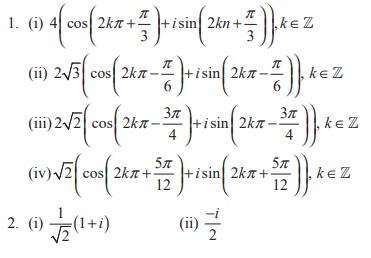
Related Topics