Chapter: 12th Mathematics : UNIT 2 : Complex Numbers
Introduction to Complex Numbers
Introduction to
Complex Numbers
Before introducing
complex numbers, let us try to answer the question ŌĆ£Whether there exists a real
number whose square is negative?ŌĆØ LetŌĆÖs look at simple examples to get the
answer for it. Consider the equations 1 and 2.
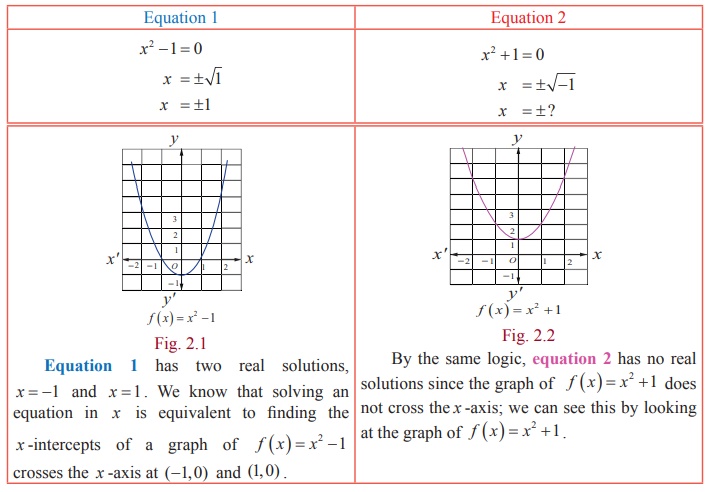
This is because, when we square a real number it is impossible to
get a negative real number.
If equation 2 has solutions, then we must create an imaginary
number as a square root of ŌłÆ1.
This imaginary unit ŌłÜŌłÆ1
is denoted by i .The imaginary number i tells us that i2 = ŌłÆ1. We can use this fact
to find other powers of i .
Powers of imaginary unit i

We note that, for any
integer n , in has only four possible values: they
correspond to values of n when divided by 4 leave the remainders 0, 1,
2, and 3.That is when the integer n Ōēż ŌłÆ4 or n Ōēź 4 , using division algorithm, n can be written as n = 4q + k, 0 Ōēż k < 4, k and q are
integers and we write
i)n = (i)4q+k = (i)4q(i)k = ((i)4)q(i)k = (i) q(i)k =(i)k
Example 2.1
Simplify the following
(i) i7 (ii) i1729 (iii) i ŌłÆ1924 + i2018 (iv) ![]() (v) i i2 i3 ŌĆ”.. i40
(v) i i2 i3 ŌĆ”.. i40
Solution
(i) (i)7 = (i)4+3 = (i)3 = -i;
(ii) i1729 = i1729i1 = i
(iii) (i)-1924 + (i)2018 = (i)-1924+0 + (i)2016+2 = (i)0 + (i)2 = 1-1 = 0
(iv) ![]() = (i1 + i2 + i3 + i4) + (i5 + i6 + i7 + i8 ) + ŌĆ” + (i97 + i98 + i99 + i100 +) + i101 + i102
= (i1 + i2 + i3 + i4) + (i5 + i6 + i7 + i8 ) + ŌĆ” + (i97 + i98 + i99 + i100 +) + i101 + i102
= (i1 + i2 + i3 + i4) + (i1 + i2 + i3 + i4) + ŌĆ” + (i1 + i2 + i3 + i4) + i1 + i2
= {i+(-1)+(-i)+1} + {i+(-1)+(-i)+1} +
ŌĆ”. ŌĆ” + {i+(-1)+(-i)+1} + i + (-1)
= 0 + 0 + ŌĆ” 0 + i -1
= ŌłÆ1 + i (What is this number?)
(v) i i2 i3 ŌĆ” i40 = i1+2+3+ŌĆ”+40 = i [40x41]/2 = i820 = i0 = 1
Note
(i) ŌłÜ[ab] = ŌłÜaŌłÜb valid only if at least one of a, b is
non-negative.
For example, 6 = ŌłÜ36 = ŌłÜ[(-4)(-9)] = ŌłÜ(-4) ŌłÜ (-9) = (2i) (3i)
= 6i2 = -6, a contradiction.
Since we have taken ŌłÜ[(-4)(-9)] = ŌłÜ(-4) ŌłÜ (-9), we arrived at a
contradiction.
Therefore ŌłÜ[ab] = ŌłÜa ŌłÜb valid only if at least one of a b,
is non-negative.
(ii) For y Ōłł R , y2 Ōēź 0
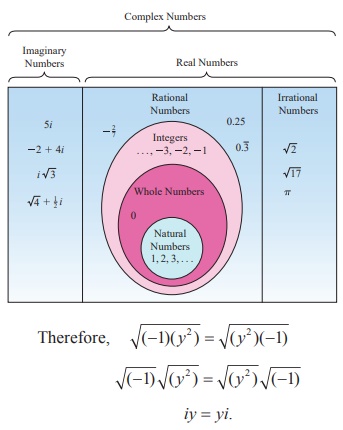
iy = yi.
Related Topics