Modulus of a Complex Number

Modulus of a Complex Number

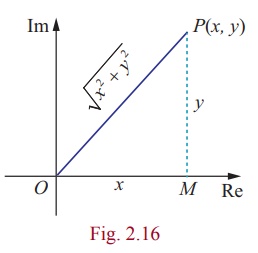
Just as the absolute value of a real number measures the distance of that number from origin along the real number line, the modulus of a complex number measures the distance of that number from the origin in the complex plane. Observe that the length of the line from the origin along the radial line to z = x + iy is simply the hypotenuse of a right triangle, with one side of length x and the other side of length y 

Definition 2.4

If z = x + iy, then the modulus of z, denoted by |z| , is defined by |z| = √[x² + y²]