Exercise 2.6: Geometry and Locus of Complex Numbers

EXERCISE 2.6

1. If z = x + iy is a complex number such that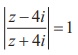 

show that the locus of z is real axis.

2. If z = x + iy is a complex number such that Im 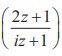 = 0 , show that the locus of z is

2x2 + 2 y2 + x - 2 y = 0.

3. Obtain the Cartesian form of the locus of z = x + iy in each of the following cases:

(i)  [Re (iz )]2 = 3  

(ii) Im[(1- i)z +1] = 0

(iii) |z + i| = |z -1|

(iv)  = z-1.

4. Show that the following equations represent a circle, and, find its centre and radius.

(i) |z - 2 – i| = 3

(ii) |2z + 2 - 4i| = 2 

(iii) |3z - 6 +12i| = 8

5. Obtain the Cartesian equation for the locus of z = x + iy in each of the following cases:

(i)  |z – 4| = 16

(ii) |z – 4|2 - |z -1|2 = 16 .

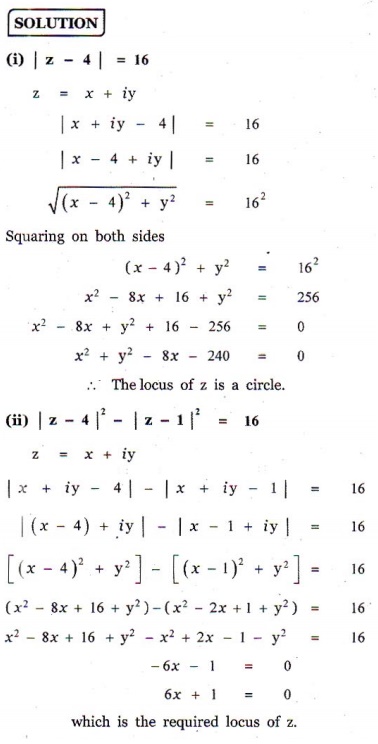
Answers: