Polar form of a complex number

Polar and Euler form of a Complex Number

When performing addition and subtraction of complex numbers, we use rectangular form. This is because we just add real parts and add imaginary parts; or subtract real parts, and subtract imaginary parts. When performing multiplication or finding powers or roots of complex numbers, use an alternate form namely, polar form, because it is easier to compute in polar form than in rectangular form.

Polar form of a complex number

Polar coordinates form another set of parameters that characterize the vector from the origin to the point z = x + iy , with magnitude and direction. The polar coordinate system consists of a fixed point O called the pole and the horizontal half line emerging from the pole called the initial line (polar axis). If r is the distance from the pole to a point P and θ is an angle of inclination measured from the initial line in the counter clockwise direction to the line OP, then r and θ of the ordered pair (r,θ ) are called the polar coordinates of P. Superimposing this polar coordinate system on the rectangular coordinate system, as shown in diagram, leads to

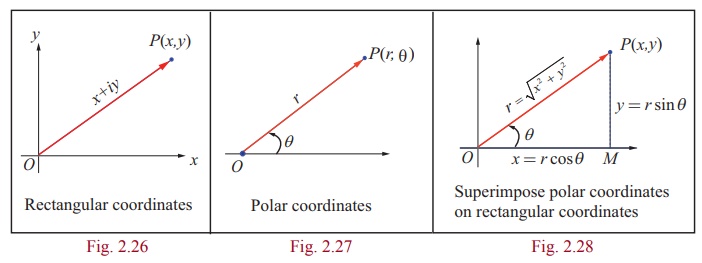
x  = r cosθ   ...(1)

y  = r sinθ        â€¦.(2)

Any non-zero complex number z = x + iy can be expressed as z = r cosθ + i r sinθ.

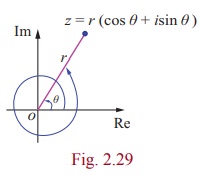
Definition 2.6

Let r and θ be polar coordinates of the point P(x, y) that corresponds to a non-zero complex number z = x + iy . The polar form or trigonometric form of a complex number P is

z = r(cosθ + i sinθ ) .

For convenience, we can write polar form as

 z = x + iy = r (cosθ + i sinθ ) = r cisθ .

The value r represents the absolute value or modulus of the complex number z . The angle θ is called the argument or amplitude of the complex number z denoted by θ = arg ( z ).

(i) If z = 0 , the argument θ is undefined; and so it is understood that z ≠ 0 whenever polar coordinates are used.

(ii) If the complex number z = x + iy has polar coordinates (r, θ ) , its conjugate  = x − iy has polar coordinates (r, −θ ) .

Squaring and adding (1) and (2), and taking square root, the value of r is given by r = |z|  =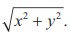  

Dividing (2) by (1),  

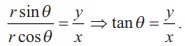
Case (i) The real number θ represents the angle, measured in radians, that z makes with the positive real axis when z is interpreted as a radius vector. The angle θ has an infinitely many  possible  values,  including  negative  ones  that  differ by integral multiples of 2Ï€. Those values can be determined from the equation tan θ = y/x where the quadrant containing the point corresponding to  z must be specified. Each value of θ is called an argument of z, and the set of all such values is obtained by adding multiple of 2Ï€ to θ, and it is denoted by arg z.

Case (ii) There is a unique value of θ which satisfies the condition −π <θ ≤ Ï€ . 

This value is called a principal value of θ or principal argument of z and is denoted by Arg z.

Note that, − Ï€ < Arg(z) ≤ Ï€  or −π < θ  ≤ Ï€

Principal Argument of a complex number

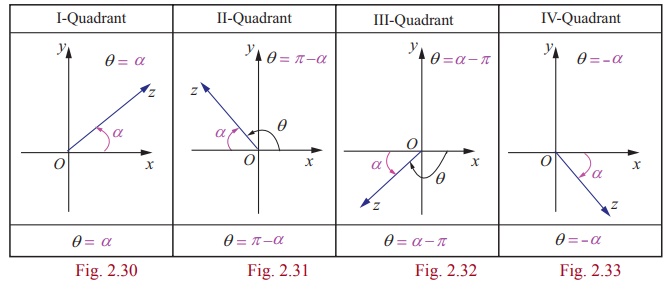
The capital A is important here to distinguish the principal value from the general value.

Evidently, in practice to find the principal angle θ, we usually compute α = tan^-1|y/x| and adjust for the quadrant problem by adding or subtracting α with π appropriately.

arg z = Arg z + 2 n Ï€,  n âˆˆ Z .

Some of the properties of arguments are

(1) arg ( z₁ z₂ ) = arg z₁ + arg z₂

(2) arg (z₁/z₂) = arg z₁ - arg z₂

(3) arg (zⁿ) = n arg  z

(4) The alternate forms of cos θ + i sin θ are cos (2kπ + θ) + i sin (2kπ + θ), k ∈ Z.

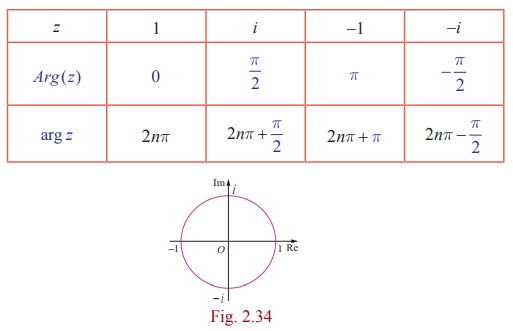
For instance the principal argument and argument of 1, i, -1, and -i are shown below:-

Illustration

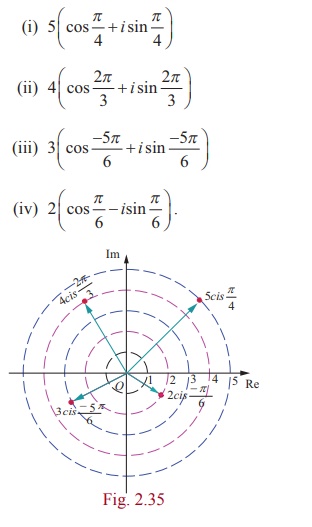
Plot the following complex numbers in complex plane