Modulus of a Complex Number: Solved Example Problems

Example 2.9

If z₁ = 3 + 4i, z₂ = 5 -12i, and z₃ = 6 + 8i, find |z₁| , |z₂|, |z₃|, |z₁ + z₂| ,| z₂ - z₃|, and |z₁ + z₃|.

Solution

Using the given values for z₁, z₂ and z₃ we get |z₁| = |3 + 4i| = √[3² +4²] =5 

|z₂|   = |5 -12i| = √[5² + (-12)²] = 13

z₃   = |6 + 8i| = √[6² + 8²] = 10

|z₁  + z₂| =  |(3 + 4i ) + (5 -12i)| = |8 - 8i| = √128 = 8√2

|z₂ - z₃| = |(5 -12i ) - (6 + 8i )| = |-1- 20i| = √401

|z₁  + z₃| =  |(3 + 4i) + (6 + 8i)| = |9 +12i| = √225 = 15

Note that the triangle inequality is satisfied in all the cases.

|z₁ + z₃| = |z₁| + |z₃|= 15 (why?)

Example 2.10

Find the following

Solution

Example 2.11

Which one of the points i, -2 + i , and 3 is farthest from the origin?

Solution

The distance between origin to z = i, -2 + i, and 3 are 

| z | = | i | = 1

| z | = | -2 + i |= √[(-2)²+(1)²] = √5

= | z | = | 3 | = 3

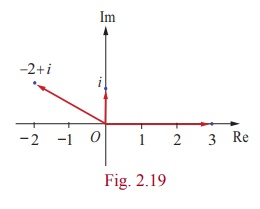
Since 1 < √5 < 3 , the farthest point from the origin is 3

Example 2.12

If z₁, z₂, and z₃ are complex numbers such that |z₁| = |z₂| =|z₃| = |z₁ + z₂ + z₃| = 1, find the value of .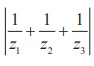

Solution

Since, |z₁| = |z₁| = |z₁| = 1,

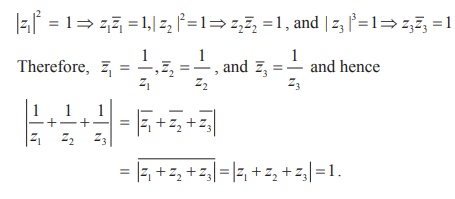
Example 2.13

If |z| = 2 show that 3 ≤ |z + 3 + 4i| ≤ 7

Solution

|z + 3 + 4i| ≤ |z| + |3 + 4i|  = 2 + 5 = 7

|z + 3 + 4i| ≤ 7      (1)

|z + 3 + 4i| ≥ | |z| - | 3 + 4i| | = |2-5| = 3

|z + 3 + 4i| ≥ 3                     (2)

From (1) and (2), we get 3 ≤ |z + 3 + 4i| ≤ 7 

Note

To find the lower bound and upper bound use | |z₁| - |z₂| | ≤ |z₁ + z₂ | ≤ |z₁| + |z₂|.

Example 2.14

Show that the points 1,  are the vertices of an equilateral triangle.

Solution

It is enough to prove that the sides of the triangle are equal.

Let z = 1, 

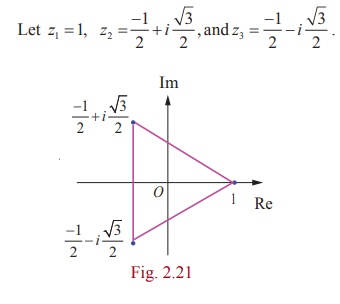
The length of the sides of the triangles are

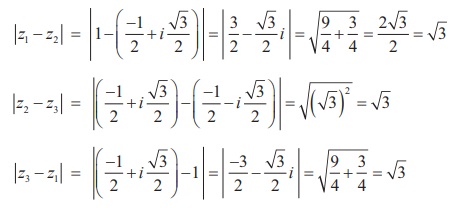
Since the sides are equal, the given points form an equilateral triangle.

Example 2.15

Let z₁ , z₂ , and z₃ be complex numbers such that |z₁| = |z₂| =|z₃| = r > 0 and z₁ + z₂ + z₃ ≠ 0 .

Prove that .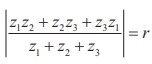

Solution

Example 2.16

Show that the equation z² =  has four solutions.

Solution

We have,

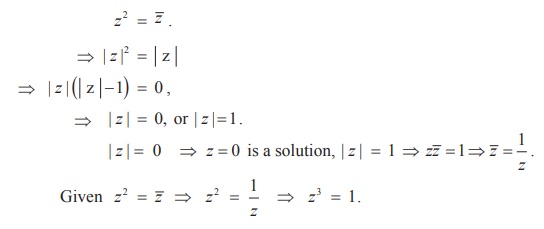
It has 3 non-zero solutions. Hence including zero solution, there are four solutions.