Definition, Formula, Solved Example Problems - de MoivreŌĆÖs Theorem and its Applications | 12th Mathematics : UNIT 2 : Complex Numbers
Chapter: 12th Mathematics : UNIT 2 : Complex Numbers
de MoivreŌĆÖs Theorem and its Applications
de MoivreŌĆÖs Theorem and its Applications
Abraham de Moivre (1667ŌĆō1754) was one of the mathematicians to
use complex numbers in trigonometry.
The formula (cos╬Ė + i sin╬Ė )n = (cos n╬Ė + i sin n╬Ė ) known by his name, was instrumental in
bringing trigonometry out of the realm of geometry and into that of analysis.

1. de Moivre's Theorem
de MoivreŌĆÖs Theorem
Given any complex number cos╬Ė + i sin╬Ė and any integer n,
(cos╬Ė + i sin╬Ė )n = cos n╬Ė
+ i sin n╬Ė .
Corollary
(1) (cos╬Ė - i sin╬Ė )n = cos n╬Ė -
i sin n╬Ė
(2) (cos╬Ė + i sin╬Ė )-n = cos n╬Ė -
i sin n╬Ė
(3) (cos╬Ė - i sin╬Ė )-n = cos n╬Ė +
i sin n╬Ė
(4) sin╬Ė + i cos╬Ė = i (cos╬Ė -
i sin╬Ė ) .
Now let us apply de MoivreŌĆÖs theorem to simplify complex numbers and to find solution of equations.
Example 2.28
If z = (cos╬Ė + i sin╬Ė ) , show that zn + 1/ zn = 2 cos n╬Ė and zn ŌĆō [1/ zn] = 2i sin n╬Ė
.
Solution
Let z = (cos╬Ė + i sin╬Ė ) .
By de MoivreŌĆÖs theorem ,
zn = (cos╬Ė + i sin╬Ė )n = cos n╬Ė + i sin n╬Ė
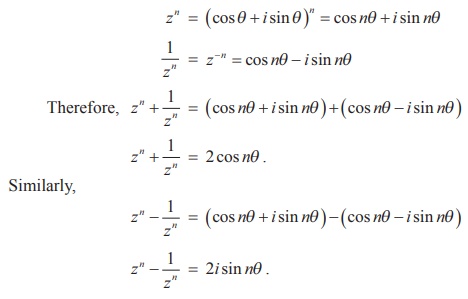
Example 2.29
Similarly, 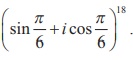
Solution
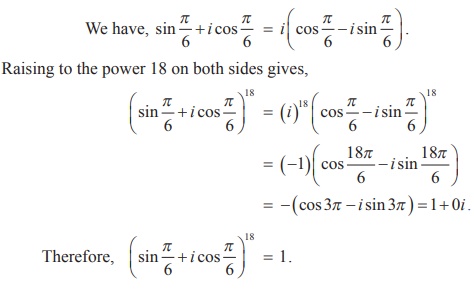
Example 2.30
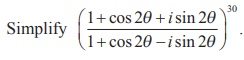
Solution

Example 2.31
Simplify
(i) (1+ i)18
(ii) (-ŌłÜ3 + 3i)31 .
Solution
(i) (1+ i)18
Let 1+ i = r (cos╬Ė + i sin╬Ė ) .
Then, we get

(ii) (-ŌłÜ3 + 3i)31 .
Let -ŌłÜ3 + 3i = r (cos╬Ė + i sin╬Ė ) .
Then, we get
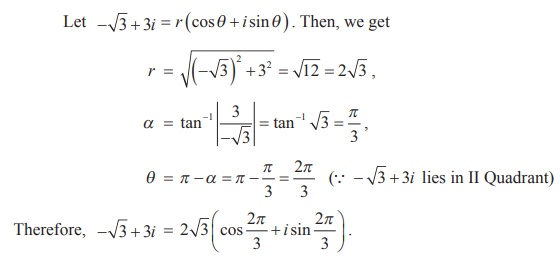
Raising power 31 on both sides,
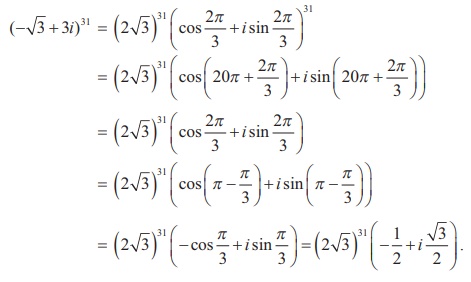
2. Finding nth roots of a complex number
de MoivreŌĆÖs formula can be used to obtain roots of complex numbers. Suppose n is a positive integer and a complex number Žē is n th root of z denoted by z1/ n , then we have
Žēn = z
ŌĆ”ŌĆ”ŌĆ”ŌĆ”(1)
Let Žē = Žü (cosŽĢ
+ i sinŽĢ ) and
z = r (cos╬Ė + i sin╬Ė ) = r (cos(╬Ė
+ 2kŽĆ ) + i sin (╬Ė + 2kŽĆ )), k Ōłł Z
Since w is the nth root of z , then
Žēn = z
ŌćÆ Žün (cosŽĢ + i sinŽĢ)n = r (cos(╬Ė + 2kŽĆ ) + i sin (╬Ė + 2kŽĆ )) , k Ōłł Z
By de MoivreŌĆÖs theorem,
ŌćÆ Žün (cosnŽĢ + i sinnŽĢ) = r (cos (╬Ė + 2kŽĆ ) + i sin (╬Ė + 2kŽĆ )), k Ōłł Z
Comparing the moduli and arguments, we get
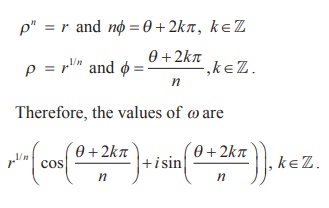
Although there are infinitely many values of k ,
the distinct values of Žē are obtained when k = 0,1,
2, 3,K, n ŌłÆ1. When k
= n, n +1, n + 2,K we get the same roots at regular intervals
(cyclically). Therefore the nth roots of complex number z = r (cos╬Ė
+ i sin╬Ė ) are
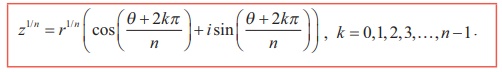
If we set Žē = 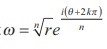 the formula for the n th roots of
a complex number has a
nice geometric interpretation, as shown in Figure. Note that because | Žē
| = nŌłÜr the n roots
all have the same modulus nŌłÜr they all lie on a circle of radius nŌłÜr with centre at the
origin. Furthermore, the n roots are equally spaced along the circle, because
successive n roots have arguments that differ by 2ŽĆ/n .
the formula for the n th roots of
a complex number has a
nice geometric interpretation, as shown in Figure. Note that because | Žē
| = nŌłÜr the n roots
all have the same modulus nŌłÜr they all lie on a circle of radius nŌłÜr with centre at the
origin. Furthermore, the n roots are equally spaced along the circle, because
successive n roots have arguments that differ by 2ŽĆ/n .
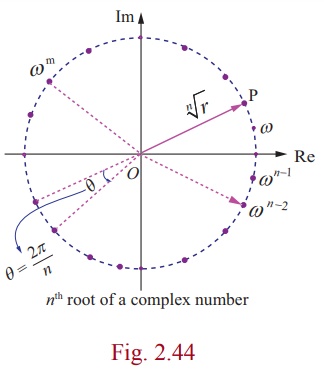
Remark
(i) General form of de Moivre's Theorem
If x is rational, then cos x╬Ė + i sin x╬Ė is one of the values
of (cos╬Ė + i sin╬Ė )x .
(ii) Polar form of unit circle
Let z = ei╬Ė = cos╬Ė + i sin╬Ė . Then, we get
|z|2 = |cos╬Ė + i sin╬Ė|2
ŌćÆ | x + iy|2 = cos2╬Ė + sin2╬Ė = 1
ŌćÆ x2 + y2 = 1.
Therefore, |z| = 1 represents a unit circle (radius one) centre
at the origin.
3. The nth roots of unity
The solutions of the equation zn = 1 , for positive values
of integer n , are the n roots of the unity.
In polar form the equation zn = 1 can be written as
zn = cos (0 + 2kŽĆ) + i sin (0 + 2kŽĆ) = ei2kŽĆ , k = 0, 1, 2,ŌĆ”..
Using deMoivreŌĆÖs theorem, we find the nth roots of unity from
the equation given below:
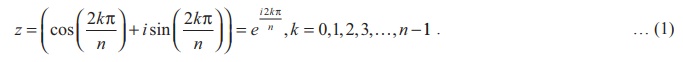
Given a positive integer n , a complex number z is
called an n th root of unity if and only if zn = 1.
If we denote the complex number by Žē , then
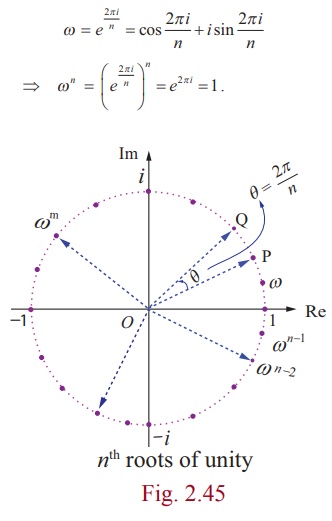
Therefore Žē is an nth root of unity. From equation (1), the complex numbers 1,Žē,Žē2 ,... ...,Žēn-1 are nth roots of unity. The complex numbers 1,Žē,Žē2 ,... ...,Žēn-1 are the points in the complex plane and are the vertices of a regular polygon of n sides inscribed in a unit circle as shown in Fig 2.45. Note that because the n th roots all have the same modulus 1, they will lie on a circle of radius 1 with centre at the origin. Furthermore, the n roots are equally spaced along the circle, because successive n th roots have arguments that differ by 2ŽĆ/n .
The nth roots of unity 1,Žē,Žē2 ,... ...,Žēn-1 are in geometric progression with common ratio
Žē
Therefore 1+ Žē + Žē2 +ŌĆ” + Žēn-1 = 1- Žēn / 1- Žē = 0 since Žēn = 1 and Žē ŌēĀ 1 .
The sum of all the nth roots of unity is
1+ Žē + Žē2 +ŌĆ” + Žēn-1 = 0
The product of n, nth roots of unit is
1ŽēŽē2 ... ...Žēn-1 = Žē0+1+2+3+... ...+(n-1) = Žē[(n-1)n]/2
The product of all the nth roots of unity is
1ŽēŽē2 ... ...Žēn-1 = (-1)n-1

Note
(1) All the n roots of nth roots unity are in Geometrical Progression
(2) Sum of the n roots of nth roots unity is always
equal to zero.
(3) Product of the n roots of nth roots unity is equal to
(-1)n-1 .
(4) All the n roots of nth roots unity lie on the circumference of a circle whose centre is at the origin and radius equal to 1 and these roots divide the circle into n equal parts and form a polygon of n sides.
Example 2.32
Find the cube roots of unity.
Solution
We have to find 11/3 . Let z = 11/3 then z3 = 1.
In polar form, the equation z3 = 1 can be written as
z3 = cos(0 + 2kŽĆ) + i sin(0 + 2kŽĆ) = ei2kŽĆ , k = 0, 1, 2,...

Example 2.33
Find the fourth roots of unity.
Solution
We have to find 11/4. Let z =11/4 . Then z4 = 1 .
In polar form, the equation z4 = 1 can be written as
z4 = cos (0 + 2kŽĆ ) + i sin (0 + 2kŽĆ ) = ei2kŽĆ , k = 0, 1,
2,...

Note
(i) In this chapter the letter Žē is used for nth roots of unity.
Therefore the value of Žē is depending on n as shown in following table.

(ii) The complex number zei╬Ė is a rotation of z by ╬Ė radians in the counter
clockwise direction about the origin.
Example 2.34
Solve the equation z3 + 8i = 0 , where z Ōłł C.
Solution
Let z3 + 8i = 0 . Then, we get
z3 = -8i
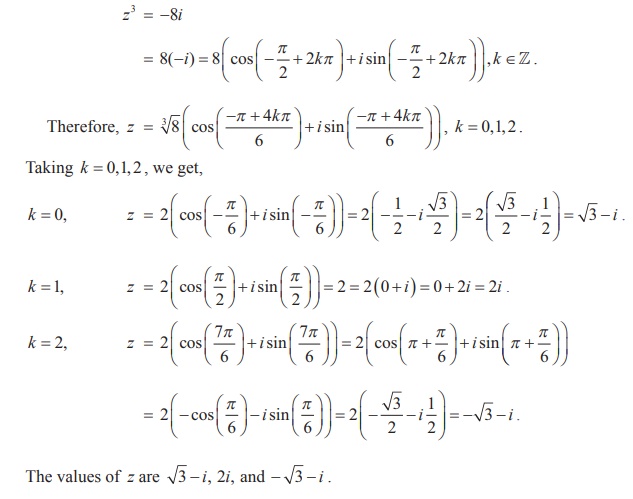
Example 2.35
Find all cube roots of ŌłÜ3 + i
Solution
We have to find (ŌłÜ3 + i)1/3. Let z3 = ŌłÜ3 + i = r (cos╬Ė + i sin╬Ė )

Example 2.36
Suppose z1 , z2, and z3 are the vertices of an equilateral triangle inscribed in the
circle |z| = 2. If z1 = 1+ iŌłÜ3 , then find z2 and z3.
Solution
|z| = 2 represents the circle with centre (0, 0) and radius 2.
Let A, B, and C be the vertices of the given triangle. Since the
vertices z1 , z2 , and z3 form an equilateral
triangle inscribed in the circle |z| = 2 , the sides of this triangle AB, BC,
and CA subtend 2ŽĆ/3 radians (120 degree) at the origin (circumcenter of the
triangle).
(The complex number z ei╬Ė is a rotation of z by ╬Ė radians in the counter
clockwise direction about the origin.)
Therefore, we can obtain z2 and z3 by the rotation of z1 by 2ŽĆ/3 and 4 ŽĆ/3
respectively.
Given that
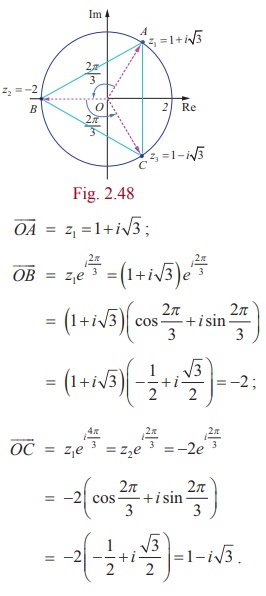
Therefore, z2 = -2, and z3 = 1- iŌłÜ3.
Related Topics