Definition, Formulas, Solved Example Problems - Square roots of a complex number | 12th Mathematics : UNIT 2 : Complex Numbers
Chapter: 12th Mathematics : UNIT 2 : Complex Numbers
Square roots of a complex number
Square roots of a complex number
Let the square root of a + ib be x + iy
That is = ŌłÜ[a+ib] = x + iy where x, y Ōłł
R
a + ib = ( x + iy )2 = x2 - y2 + i2xy
Equating real and imaginary parts, we get
x2 - y 2 = a and 2xy = b
(x2 + y2 )2 = (x2 - y2 ) 2 + 4x2 y2 = a2 + b2
x2 + y2 = ŌłÜ[a2+b2], since x2 + y2 is positive
Solving x2 + y2 = a and
x2+ y2 =ŌłÜ[a2+b2], we get
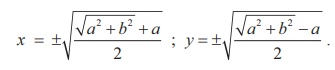
Since 2xy = b it is clear that both x and
y will have the same sign when b is positive, and x and y
have different signs when b is negative.
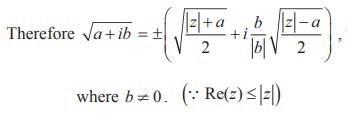
Formula for finding
square root of a complex number
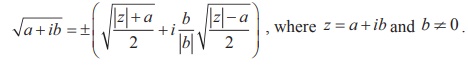
Note
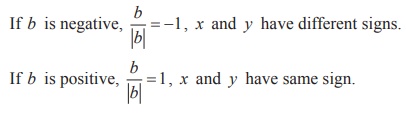
Example 2.17
Find the square root of 6 - 8i.
Solution
We compute |6 - 8i| = ŌłÜ[62 + (-8)2] = 10
and applying the formula for square root, we get
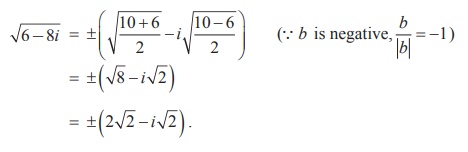
Related Topics