Complex Numbers - Summary | 12th Mathematics : UNIT 2 : Complex Numbers
Chapter: 12th Mathematics : UNIT 2 : Complex Numbers
Summary
SUMMARY
In this chapter we studied
Rectangular form of a complex number is x + iy (or x + yi) ,
where x and y are real numbers.
Two complex numbers z1 = x1 + iy1 and z2 = x2 + iy2 are said to be equal
if and only if
Re(z1 ) = Re(z2 ) and
Im(z1 ) = Im(z2 ) . That is x1 = x2 and y1 = y2 .
The conjugate of the complex number x + iy is
defined as the complex number x - iy.
Properties of complex conjugates

If z = x + iy, then ŌłÜ[x2 + y2] is called modulus of z . It is denoted
by |z| .
Properties of Modulus of a complex number
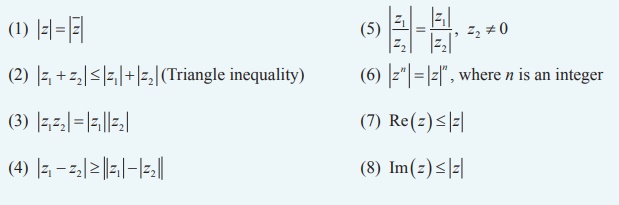
Formula for finding square root of a complex number

Let r and ╬Ė be polar coordinates
of the point P(x, y) that corresponds to a non-zero complex
number z
= x + iy . The polar form or
trigonometric form of a complex number P is
z = r(cos╬Ė + i sin╬Ė ) .
Properties of polar form
Property 1:
If z = r (cos╬Ė
+ i sin╬Ė ), then z-1 = 1/r (cos╬Ė - i sin╬Ė )
.
Property 2:
If z1 = r1 (cos╬Ė1 + i sin╬Ė1 ) and z2 = r2 (cos╬Ė2 + i sin╬Ė2 ),
then z1 z2 = r1r2 (cos(╬Ė1 + ╬Ė2 ) + i sin(╬Ė1 + ╬Ė2 )) .
Property 3:
If z1 = r1 (cos╬Ė1 + i sin╬Ė1 ) and z2 = r2 (cos╬Ė2 + i sin╬Ė2 ) ,
Then z1/z2 = r1/r2 [cos(╬Ė1- ╬Ė2) + i sin(╬Ė1- ╬Ė2) ]
de MoivreŌĆÖs Theorem
(a) Given any complex
number cos
╬Ė + i sin
╬Ė and any integer n,
(cos╬Ė + i sin╬Ė
)n = cos n╬Ė + i sin n╬Ė
(b) If x is rational, then cos x ╬Ė + i sin
x ╬Ė in one of the values of (cos ╬Ė + i sin ╬Ė)x
The nth roots of complex number z = r (cos╬Ė
+ i sin╬Ė ) are
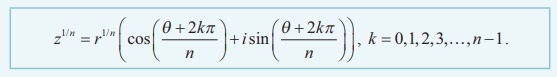
Related Topics