Complex Numbers

Complex Numbers

We have seen that the equation x² +1 = 0 does not have a solution in real number system.

In general there are polynomial equations with real coefficient which have no real solution.

We enlarge the real number system so as to accommodate solutions of such polynomial equations.

This has triggered the mathematicians to define complex number system.

In this section, we define

a)           Complex numbers in rectangular form

b)          Argand plane

c)           Algebraic operations on complex numbers

The complex number system is an extension of real number system with imaginary unit i .

The imaginary unit i with the property i² = −1 , is combined with two real numbers x and y by the process of addition and multiplication, we obtain a complex number x + iy. The symbol '+ ' is treated as vector addition. It was introduced by Carl Friedrich Gauss (1777-1855).

1. Rectangular form

Definition 2.1 (Rectangular form of a complex number)

A complex number is of the form x + iy (or x + yi) , where x and y are real numbers. x is called the real part and y is called the imaginary part of the complex number.

If x = 0 , the complex number is said to be purely imaginary. If y = 0 , the complex number is said to be real. Zero is the only number which is at once real and purely imaginary. It is customary to denote the standard rectangular form of a complex number x + iy as z and we write x = Re(z) and y = Im(z) . For instance, Re(5 − i7) = 5 and Im (5 − i7) = −7 .

The numbers of the form α + iβ , β ≠ 0 are called imaginary (non real complex) numbers.

The equality of complex numbers is defined as follows.

Definition 2.2

Two complex numbers z₁ = x₁ + iy₁ and z₂ = x₂ + iy₂ are said to be equal if and only if

Re(z₁ ) = Re(z₂ )  and  Im(z₁ ) = Im(z₂) . That is  x₁ = x₂ and y₁ = y₂ .

For instance, if α + iβ = −7 + 3i , then α = −7 and β = 3 .

2. Argand plane

A complex number z = x + iy is uniquely determined by an ordered pair of real numbers ( x, y ) .

The numbers 3 − 8i, 6 and −4i are equivalent to (3, −8), (6, 0), and (0, −4) respectively. In this way we are able to associate a complex number z = x + iy with a point ( x, y ) in a coordinate plane.

If we consider x axis as real axis and y axis as imaginary axis to represent a complex number, then the xy -plane is called complex plane or Argand plane. It is named after the Swiss mathematician Jean Argand (1768 – 1822).

A complex number is represented not only by a point, but also by a position vector pointing from the origin to the point. The number, the point, and the vector will all be denoted by the same letter z . As usual we identify all vectors which can be obtained from each other by parallel displacements. In this chapter, C denotes the set of all complex numbers. Geometrically, a complex number can be viewed as either a point in R² or a vector in the Argand plane.

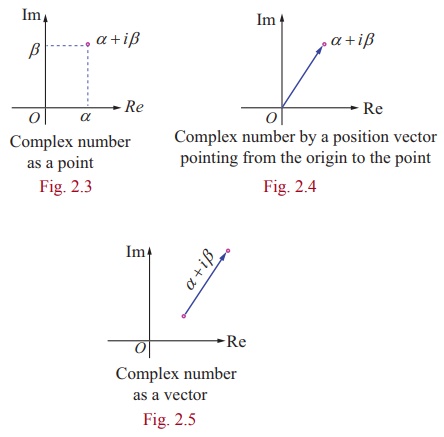
Illustration 2.1

Here are some complex numbers: 2 + i, − 1 + 2i, 3 - 2 i, 0 - 2 i, 3+ √-2, -2-3i, cos (Ï€/6) + isin(Ï€/6) and 3  + 0i. Some of them are plotted in Argand plane. 

3. Algebraic operations on complex numbers

In this section, we study the algebraic and geometric structure of the complex number system.

We assume various corresponding properties of real numbers to be known.

(i) Scalar multiplication of complex numbers:

If z = x + iy and k ∈ R, then we define

k z = (kx) + (ky )i .

In particular 0 z = 0 , 1 z = z and (−1)z = −z .

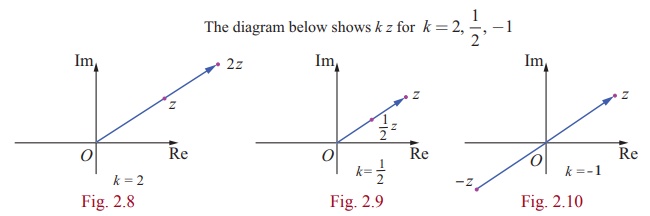
(ii) Addition of complex numbers:

If z₁ = x₁ + iy₁ and z₂ = x₂ + iy₂ , where x₁ , x₂ , y₁ , and y₂ ∈ R, then we define

z₁ + z₂ = (x₁ + iy₁) + (x₂ + iy₂)

= (x₁ + x₂) + i(y₁ + y₂)

z₁ + z₂= (x₁ + x₂) + i(y₁ + y₂)

We have already seen that vectors are characterized by length and direction, and that a given vector remains unchanged under translation.   When z₁ = x₁ + iy₁      and    z₂  = x₂  + iy₂ then  by  the parallelogram law of addition,thesum  z₁  + z₂ = ( x₁  + x₂ ) + i ( y₁  + y₂ ) corresponds to the point ( x₁ + x₂ , y₁ + y₂ ) .  It also corresponds to a vector with those coordinates as its components. Hence the points z₁ , z₂ , and z₁ + z₂ in complex plane may be obtained vectorially as shown in the adjacent Fig. 2.11.

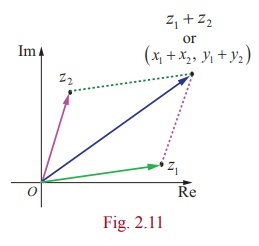
iii) Subtraction of complex numbers

Similarly the difference z₁ − z₂ can also be drawn as a position vector whose initial point is the origin and terminal point is ( x₁ − x₂ , y₁ − y₂ ) . We define

z₁ - z₂ = z₁ + (- z₂  )

= (x₁ + iy₁) + (-x₂ - iy₂)

= (x₁ - x₂) + i(y₁ - y₂)

z₁ + z₂= (x₁ - x₂) + i(y₁ - y₂)

It is important to note here that the vector representing the difference of the vector z₁ − z₂ may also be drawn joining the end point of z₂ to the tip of z₁ instead of the origin. This kind of representation does not alter the meaning or interpretation of the difference operator. The difference vector joining the tips of z₁ and z₂ is shown in (green) dotted line.

(iv) Multiplication of complex numbers

The multiplication of complex numbers z1 and z2 is defined as

z₁ z₂ = (x₁ + iy₁ )(x₂ + iy₂ )

= (x₁ x₂ − y₁ y₂ ) + i(x₁ y₂ + x₂ y₁ )

z₁ z₂ = (x₁ x₂ − y₁ y₂ ) + i(x₁ y₂ + x₂ y₁ ) .

Although the product of two complex numbers z₁ and z₂ is itself a complex number represented by a vector, that vector lies in the same plane as the vectors z₁ and z₂ . Evidently, then, this product is neither the scalar product nor the vector product used in vector algebra.

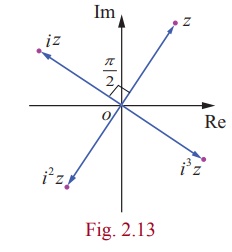
Remark

Multiplication of complex number z by i

If z  =  x + iy , then

iz = i(x + iy)

=  âˆ’ y + ix

The complex number iz is a rotation of z by 90Ëš or Ï€/2 radians in the  counter clockwise direction about the origin. In general, multiplication of a complex number z by i successively gives a 90° counter clockwise rotation successively about the origin.

Illustration 2.2

Let z₁ = 6 + 7i and z₂ = 3 − 5i . Then z₁ + z₂ and z₁ − z₂ are

(i) (3 - 5i) + (6 + 7i) = (3 + 6) + (-5+7)i = 9+2i

(6 + 7i) - (3 - 5i)  = (6 - 3) + (7 - (-5))i = 3+12i

Let z₁ = 2 + 3i and z₂ = 4 + 7i . Then z₁ z₂ is

(ii) (2 + 3i)( 4 + 7i) = (2x4 – 3x7) + i(2x7 + 3x4)

= (8-21) + (14+12)i = -13 +26i

Example 2.2

Find the value of the real numbers x and y, if the complex number (2 + i)x + (1− i) y + 2i − 3 and x + (−1+ 2i) y +1+ i are equal

Solution

Let  z₁ = (2 + i)x + (1- i) y + 2i - 3 = (2x + y - 3) + i ( x - y + 2) and

z2 = x + (-1+ 2i) y +1+ i = ( x - y +1) + i (2 y +1).

Given that z₁ = z₂ .

Therefore (2x + y - 3) + i ( x - y + 2) = ( x - y +1) + i (2 y +1) . 

Equating real and imaginary parts separately, gives

2x + y - 3=  x - y +1 ⇒ x + 2 y = 4 .

x - y + 2 = 2 y +1 ⇒ x - 3y = -1 .

Solving the above equations, gives

x = 2  and  y = 1.