Chapter: 12th Mathematics : UNIT 2 : Complex Numbers
Properties of Modulus of a complex number
Properties of Modulus of a complex number

Let us prove some of the properties.
Property
Triangle inequality
For any two complex numbers z1 and z2, we have |z1 + z2| Ōēż |z1| + |z2|.
Proof

ŌćÆ |z1 + z2|2 Ōēż (|z1| + |z2|)2
ŌćÆ |z1 + z2| Ōēż |z1| + |z2|
Geometrical interpretation
Now consider the triangle shown in figure with vertices O, z1 or z2 , and z1 + z2. We know from geometry
that the length of the side of the triangle corresponding to the vector z1 + z2 cannot be greater than
the sum of the lengths of the remaining two sides. This is the reason for calling the
property as "Triangle Inequality".

It can be generalized by means of mathematical induction to finite number of terms:
|z1 + z2 + z3 + ŌĆ”. + zn | Ōēż |z1| + |z2| + |z3| + ŌĆ” + |zn| for n = 2,3,ŌĆ”.
Property
The distance between the two points z1 and z2 in complex plane is | z1 ŌłÆ z2 |
If z1 = x1 + iy1 and z2 = x2 + iy2 , then
| z1 - z2| = | ( x1 - x2 ) + ( y1 - y2 )i|
= ŌłÜ [( x1 - x2 )2 + ( y1 - y2 )2]
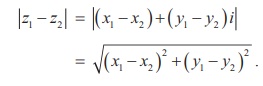
Remark
The distance between the two points z1 and z2 in complex plane is | z1 - z2 |
If we consider origin, z1 and z2 as vertices of a
triangle, by the similar argument we have
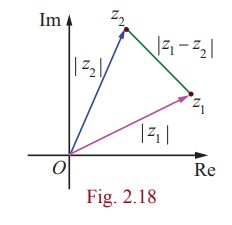
|z1 - z2| Ōēż |z1| + |z2|
| |z1| - |z2| | Ōēż | z1 + z2| Ōēż |z1| + |z2| and
| |z1| - |z2| | Ōēż | z1 - z2| Ōēż |z1| + |z2|
Property
Modulus of the product is equal to product of the moduli.
For any two complex numbers z1 and z2, we have |z1 z2| = |z1| |z2|
Proof
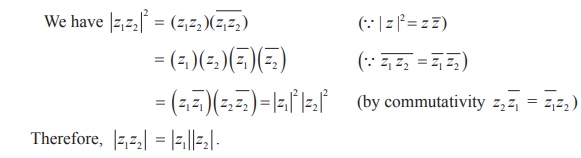
Note:
It can be generalized by means of mathematical induction to any
finite number of terms:
|z1 z2 z3 ŌĆ”.. zn| = |z1| |z2| |z3| ŌĆ” ŌĆ” |zn|
That is the modulus value of a product of complex numbers is equal
to the product of the moduli of complex numbers.
Similarly we can prove the other properties of modulus of a
complex number.
Related Topics