Definition, Properties, Formulas, Solved Example Problems - EulerŌĆÖs Form of the complex number | 12th Mathematics : UNIT 2 : Complex Numbers
Chapter: 12th Mathematics : UNIT 2 : Complex Numbers
EulerŌĆÖs Form of the complex number
EulerŌĆÖs Form of the
complex number
The following identity is known as EulerŌĆÖs formula
ei╬Ė = cos╬Ė + i sin╬Ė
Euler formula gives
the polar form z = r ei╬Ė
Note
When performing multiplication or finding powers or roots of
complex numbers, Euler form can also be used.
Example 2.22
Find the modulus and principal argument of the following complex
numbers.
(i) ŌłÜ3 + i
(ii) -ŌłÜ3 + i
(iii) - ŌłÜ3 - i
(iv) ŌłÜ3 - i
Solution
(i) ŌłÜ3 + i
Modulus =

Since the complex number has the principal value ŌłÜ3 + i
lies in the first quadrant, has the principal value
╬Ė = ╬▒ = ŽĆ/6.
Therefore, the modulus and principal argument of ŌłÜ3 + i are
2 and ŽĆ/6 respectively.
(ii) -ŌłÜ3 + i
Modulus = 2 and
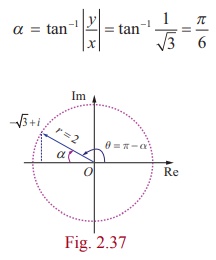
Since the complex number -ŌłÜ3 + i lies in the second
quadrant has the principal value
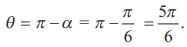
Therefore the modulus and principal argument of (ii) -ŌłÜ3 + i
are 2 and 5ŽĆ/6 respectively.
(iii) - ŌłÜ3 - i
r = 2 and ╬▒ = ŽĆ /6 .
Since the complex number - ŌłÜ3 - i lies in the third
quadrant, has the principal value,

Therefore, the modulus and principal argument of - ŌłÜ3 - i
are 2 and -5ŽĆ/6 respectively.
(iv) ŌłÜ3 - i
r = 2 and ╬▒ = ŽĆ/6
Since the complex number lies in the fourth quadrant, has the
principal value,
╬Ė = -╬▒ = -ŽĆ/6
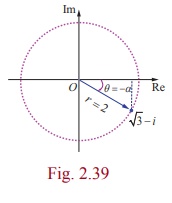
Therefore, the modulus and principal argument of
ŌłÜ3 - i are 2 and - ŽĆ/6 .
In all the four cases, modulus are equal, but the arguments are
depending on the quadrant in which the complex number lies.
Example 2.23
Represent the complex number (i) -1- i (ii) 1+ iŌłÜ3
in polar form.
Solution
(i) Let -1- i = r(cos╬Ė + isin╬Ė )
We have
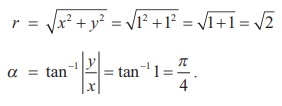
Since the complex number -1- i lies in the third quadrant, it has
the principal value,

Note
Depending upon the various values of k , we get various
alternative polar forms.
(ii) 1+ iŌłÜ3
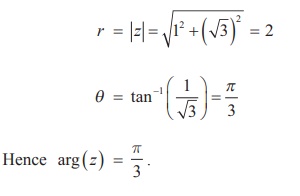
Therefore, the polar form of 1+ iŌłÜ3 can be written as

Example 2.24
Find the principal argument Arg z , when z = -2 / [ 1+iŌłÜ3 ].
Solution

This implies that one of the values of arg z is 2ŽĆ/3 .
Since 2ŽĆ/3 lies between -ŽĆ and ŽĆ, the principal argument Arg z is
2 ŽĆ/3.
Properties of polar form
Property 1
If z = r (cos╬Ė + i sin╬Ė ), then z-1 =1/r (cos╬Ė - i sin╬Ė ) .
Proof
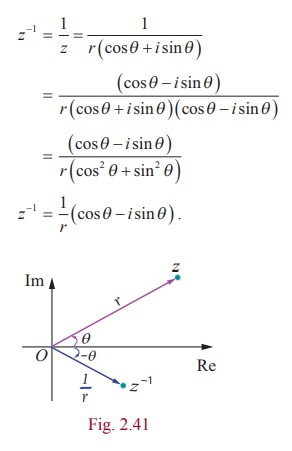
Property 2
If z1 = r1 (cos╬Ė1 + i sin╬Ė1 ) and z2 = r2 (cos╬Ė2 + i sin╬Ė2 ) ,
then z1 z2 = r1r2 (cos (╬Ė1 + ╬Ė2 ) + i sin (╬Ė1 + ╬Ė2 )) .
Proof
z = r (cos╬Ė1 + i sin╬Ė1) and
z = r (cos╬Ė2 + i sin╬Ė2)
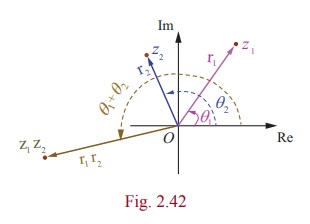
ŌćÆ z1 z2 = r1 (cos╬Ė1 + i sin╬Ė1 ) r2 (cos╬Ė2 + i sin╬Ė2 )
= r1r2 ((cos╬Ė1 cos╬Ė2 - sin╬Ė1 sin╬Ė2 ) + i (sin╬Ė1 cos╬Ė2 + sin╬Ė2 cos╬Ė1 ))
z1 z2 = r1r2 (cos (╬Ė1 + ╬Ė2 ) + i sin (╬Ė1 + ╬Ė2 )) .
Note
arg ( z1 z2 ) = ╬Ė1 + ╬Ė2 = arg ( z1 ) + arg ( z2 ) .
Property 3

Proof
Using the polar form of z1 and z2, we have
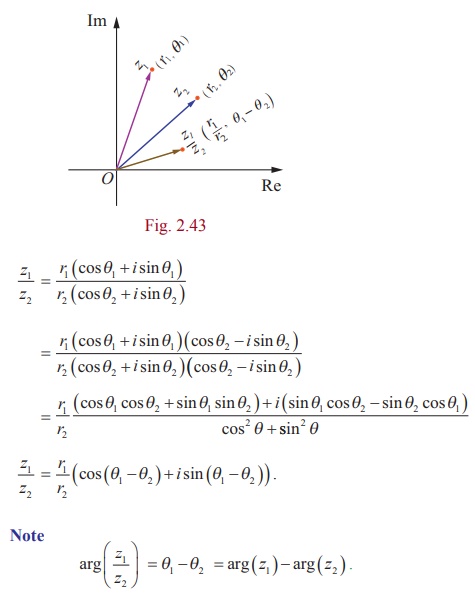
Example 2.25
Find the product  in rectangular from.
in rectangular from.
Solution

Example 2.26
Find the quotient 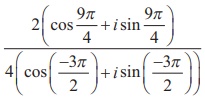 in rectangular form.
in rectangular form.
Solution
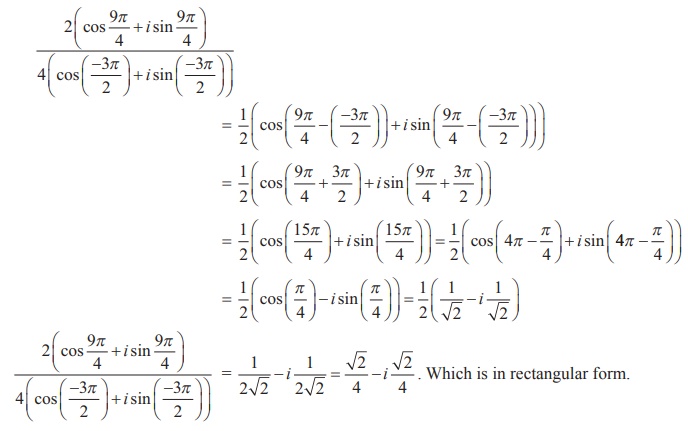
Which is in rectangular form.
Example 2.27
If z = x + iy and 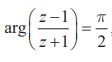 , show that x2 + y2 =1.
, show that x2 + y2 =1.
Solution
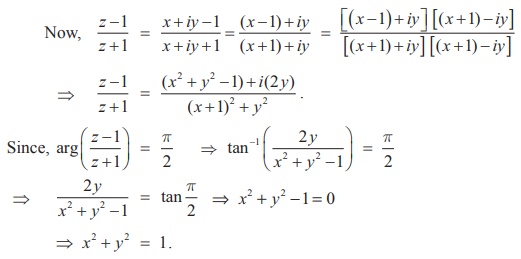
ŌćÆ x2 + y2 =1
Related Topics