Chapter: 12th Mathematics : UNIT 2 : Complex Numbers
Basic Algebraic Properties of Complex Numbers
Basic Algebraic Properties of Complex Numbers
The properties of
addition and multiplication of complex numbers are the same as for real
numbers. We list here the basic algebraic properties and verify some of them.
Properties of complex numbers

Let us now prove some
of the properties.
Property
The commutative
property under addition
For any two complex
numbers z1 and z2 , we have z1 + z2 = z2 + z1.
Proof
Let z1 = x1 + iy1 , z2 = x2 + iy2 , and x1 , x2 , y1 , and y2 Ōłł R ,
z1 + z2 = ( x1 + iy1 ) + ( x2 + iy2 )
= ( x1 + x2 ) + i ( y1 + y2 )
= ( x2 + x1 ) + i ( y2 + y1 )
(since x1 , x2 , y1 , and y2 Ōłł R )
= ( x2 + iy2 ) + ( x1 + iy1 )
= z2 + z1.
Property
Inverse Property under multiplication
Prove that the multiplicative inverse of a nonzero complex
number z = x + iy is
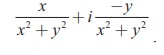
Proof
The multiplicative inverse is less obvious than the additive
one.
Let zŌłÆ1 = u + iv be the inverse of z = x + iy
We have z z-1 = 1
That is ( x + iy )(u + iv) = 1
( xu - yv) + i(xv + uy) = 1+ i0
Equating real and imaginary parts we get
xu - yv = 1and xv + uy = 0 .
Solving the above system of simultaneous equations in u and
v

Note that the above example shows the existence of z-1 of the complex number z
. To compute the inverse of a given complex number, we conveniently use z-1 = 1/z. If z1 and z2 are two complex
numbers where z2 ŌēĀ 0, then the product of z1 and 1/ z1 is denoted by z1/z2. Other properties can
be verified in a similar manner. In the next section, we define the conjugate
of a complex number. It would help us to find the inverse of a complex number
easily.
Complex numbers obey the laws of indices
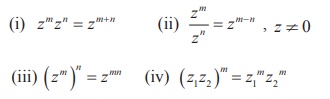
Related Topics