Geometry and Locus of Complex Numbers

Geometry and Locus of Complex Numbers

In this section let us study the geometrical interpretation of complex number z in complex plane and the locus of z in Cartesian form.

Example 2.18

Given the complex number z = 3 + 2i, represent the complex numbers z, iz, and z + iz in one Argand diagram. Show that these complex numbers form the vertices of an isosceles right triangle.

Solution

Given that z = 3 + 2i.

Therefore, iz = i (3 + 2i ) = -2 + 3i 

z + iz = (3 + 2i ) + i (3 + 2i ) = 1+ 5i

Let A, B, and C be z, z + iz, and iz respectively.

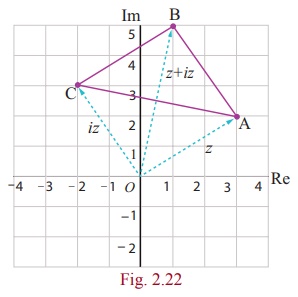
AB² = | ( z + iz ) - z|² = |-2 + 3i|² = 13

BC² = | iz - ( z + iz )|² = |-3 - 2i|² = 13

CA² = | z – iz|² = |5 – i|² = 26

Since AB² + BC² = CA² and AB = BC , ΔABC is an isosceles right triangle.

Definition 2.5 (circle)

A circle is defined as the locus of a point which moves in a plane such that its distance from a fixed point in that plane is always a constant. The fixed point is the centre and the constant distant is the radius of the circle.

Equation of Complex Form of a Circle

The locus of z  that satisfies the equation |z – z₀| = r where z₀  is a fixed complex number and r is a fixed positive real number consists of all points z whose distance from z₀ is r .

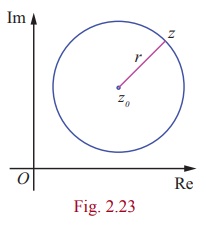
Therefore |z − z₀| = r is the complex form of the equation of a circle. (see Fig. 2.23)

(i) |z - z₀| < r represents the points interior of the circle.

(ii) |z - z₀| > r represents the points exterior of the circle.

Illustration 2.3

|z| = r ⇒ √[x² + y²] = r 

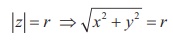
⇒ x² + y² = r² , represents a circle centre at the origin with radius r units.

Example 2.19

Show that |3z - 5 + i  | = 4 represents a circle, and, find its centre and radius.

Solution

The given equation |3z - 5 + i  | = 4 can be written as

It is of the form |z - z₀| = r and so it represents a circle, whose centre and radius are ( 5/3 , - 1/3) and 4/3 respectively.

Example 2.20

Show that |z + 2 – i| < 2 represents interior points of a circle. Find its centre and radius.

Solution

Consider the equation | z + 2 −i | = 2. 

This can be written as | z − (−2 + i)| = 2 .

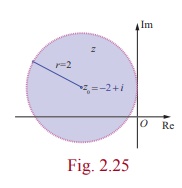
The above equation represents the circle with centre z₀ = -2 + i and radius r = 2. Therefore |z + 2 – i| < 2 represents all points inside the circle with centre at -2 + i and radius 2 as shown in figure.

Example 2.21

Obtain the Cartesian form of the locus of z in each of the following cases.

(i) |z| = |z – i|

(ii) |2z - 3 – i| = 3

Solution

(i) we have | z | = |z – i|

⇒  x + iy| = |x + iy – i|

⇒ √[x² + y²] = √ [x² + (y – 1)²]

⇒ x² + y² = x² + y² - 2y +1

⇒ 2y -1 = 0 .

(ii) we have |2z - 3 – i| = 3

|2 ( x + iy ) - 3 – i| = 3

Squaring on both sides, we get

| (2x - 3) + (2y -1)i|² = 9

⇒ (2x - 3)² + (2y -1)² = 9

⇒ 4x² + 4y² -12x - 4y +1 = 0 , the locus of z in Cartesian form