Chapter: 11th 12th std standard Class Physics sciense Higher secondary school College Notes
de Broglie wavelength of matter waves and an electron
Matter waves
The radiant energy has dual aspects of particle and wave, hence a
natural question arises, if radiation has a dual nature, why not the matter. In
1924, a French Physicist Louis de Broglie put forward the bold hypothesis that
moving particles should possess wave like properties under suitable conditions.
He reasoned this idea, from the fact, that nature is symmetrical and hence the
basic physical entities
- matter and energy should have symmetrical characters. If
radiation shows dual aspects, so should matter.
de Broglie's wavelength of matter waves
de Broglie equated the energy equations of
Planck (wave) and Einstein (particle).
For a
wave of frequency ν, the
energy associated with each photon is given by Planck's relation,
E = hν …………… (1)
where h
is Planck's constant.
According to
Einstein's mass energy
relation, a mass m
is equivalent to energy,
E = mc2 …………… (2)
where c is the velocity
of light.
If, hv = mc2
hc/ λ = mc2
or
λ = h/mc
For a particle moving with a velocity v, if c = v
from equation (3)
λ = h/mv = h/p
where p = mv, the
momentum of the particle. These hypothetical matter waves will have appreciable
wavelength only for very light particles.
de Broglie wavelength of an electron
When an electron of mass m and charge e is accelerated through a potential difference V, then the energy eV is equal to kinetic energy of the electron.
½ mv2 = eV
v = 2eV / rt(m)
The de Broglie wavelength is ,
λ = h/mv
Substituting the value of v
λ = h/ rt(2meV) ……….. (2)
Substituting the known values in equation (2),
λ = 12.27/rt(V) A0
If V = 100 volts, then λ = 1.227 Å i.e., the wavelength associated with an electron
accelerated by 100 volts is 1.227 Å.
Since E = eV is kinetic energy associated with
the electron, the equation (2) becomes,
λ = h/ rt(2mE)
Wave mechanical concept of atom
According to de Broglie's hypothesis, an
electron of mass m in motion with a
velocity v is associated with a wave
whose wavelength λ is given
by
λ =
h / mv
where h is Planck's constant.
On the basis of de Broglie's hypothesis, an atom model was proposed
in which the stationary orbits of Bohr's model were retained, but with the
difference that electron in various orbits behaves as a wave. This is shown in
Fig.
It was suggested that stationary orbits are those in which orbital
circumference (2πr) is an
integral multiple of de Broglie wavelength λ,
i.e., stationary orbits for an electron are those which contain the
complete waves of electron.
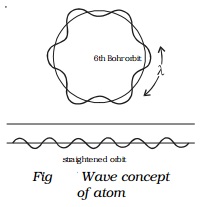
Thus, 2πr = nλ …(2)
where n = 1, 2, 3 … and r is the radius of the
circular orbit. Substituting equation (1) in equation (2),
2πr = nλ(h/mv)
mvr = nh/2π
From equation (3), it is seen that the total
angular momentum of the moving electron is an integral multiple of h/2π Thus, de Broglie's concept confirms the Bohr's postulate.
Related Topics