Physics - Work, Energy and Power: Important Questions | 11th Physics : UNIT 4 : Work, Energy and Power
Chapter: 11th Physics : UNIT 4 : Work, Energy and Power
Work, Energy and Power: Important Questions
Short Answer
Questions
1.
Explain how the definition of work in physics is different from general
percep-tion.
2.
Write the various types of potential energy. Explain the formulae.
3.
Write the differences between conservative and Non-conservative forces. Give
two examples each.
4.
Explain the characteristics of elastic and inelastic collision.
5.
Define the following
a)
Coefficient of restitution
b)
Power
c)
Law of conservation of energy
d)
loss of kinetic energy in inelastic collision.
Long Answer
Questions
1.
Explain with graphs the difference between work done by a constant force and by
a variable force.
2.
State and explain work energy principle. Mention any three examples for it.
3.
Arrive at an expression for power and velocity. Give some examples for the
same.
4.
Arrive at an expression for elastic collision in 1 Dimension and discuss
various cases.
5.
What is inelastic collision? In which way it is different from elastic
collision. Mention few examples in day to day life for inelastic collision.
Numerical Problems
1. Calculate the work done by a force of 30 N in lifting a load of 2kg to a height of 10m (g = 10ms-2)
Answer:
Given :
Force mg = 30 N ; height = 10 m
Work done to lift a load W = ?
W = F.S (or) mgh
= 30x10
W = 300 J
Ans: 300J
2. A ball with a velocity of 5 m s-1 impinges at angle of 60˚ with the vertical on a smooth horizontal plane. If the coefficient of restitution is 0.5, find the velocity and direction after the impact.
Answer
The impluse on the ball acts perpendicular to the smooth plane.
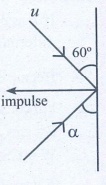
(i) The component of velocity of ball parallel to the surface.
(ii) For the component of velocity of ball perpendicular to the surface, apply law of restitution.
The component of velocity parallel to the surface will be changed.
v cos α = u cos 60°
v cos α = 5 × 1/2 = 5/2 ….(1)
According to law of restitution
v sin α = e u sin 60°
v sin α = 1/2 × 5 × √3/2 = 5 (√3/4) ….(2)
Squaring and adding (1) and (2)
v2 (sin2α + cos2α) =
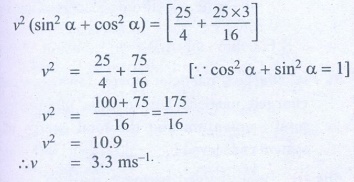
v = 3.3 ms-1
Ans: v = 0.3 m s-1
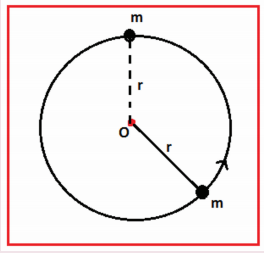
3. A bob of mass m is attached to one end of the rod of negligible mass and length r, the other end of which is pivoted freely at a fixed center O as shown in the figure. What initial speed must be given to the object to reach the top of the circle? (Hint: Use law of conservation of energy). Is this speed less or greater than speed obtained in the section 4.2.9?
Ans: √4gr ms-1
Answer
The horizontal distance, draw the point of projection to the point where the ball returns to the same level
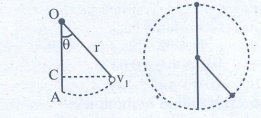
AC = OA-OC = r - rcosθ
minimum velocity = at vL = √[5gr]
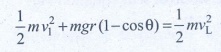
v12 = vL2 - 2gr (1 - cos θ)
v12 = 5gr - 2gr (l-cosθ)
If θ = 60°
v12 = 5gr-2gr(l – 1/2)
v12 = 5gr - gr => v12 = 4gr
v1 = √[4gr] ms-1.
4. Two different unknown masses A and B collide. A is initially at rest when B has a speed v. After collision B has a speed v/2 and moves at right angles to its original direction of motion. Find the direction in which A moves after collision.
Answer:
Momentium is censerved in both × and y direction.
In x - direction
MBVB = O + MAVA' cosɸ ...(l)
In y - direction
O = MBVB' - MAVA'sinɸ ...(2)
(2)/(1) tanɸ = VB’/VB = 1/2
tan ɸ = ½
ɸ = 26.6° (or) 26° 36' [1° = 60']
Ans: θ = 26° 33′
5. A bullet of mass 20 g strikes a pendulum of mass 5 kg. The centre of mass of pendulum rises a vertical distance of 10 cm. If the bullet gets embedded into the pendulum, calculate its initial speed.
Answer
Mass of the bullet m1 = 20 g = 0.02 kg.
Mass of the pendulum m2 = 5 kg
Centre of mass of pendulum rises to a height = h = 10 cm = 0.1 m
Speed of the bullet = u1
Pendulum is at rest .:. u2 = 0
Common velocity of the bullet and the pendulum after the bullet is embeded into the object = v
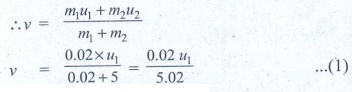
From II equation of motion
v = √[2gh] = √[2x9.8x0.1] = √[1.96] = 1.4 ms-1
Substitute the value of v in equation (1)
1.4 = 0.02 u1/5.02
u1 = 5.02x1.4 / 0.02
u1 = 351.4 ms-1
Ans: v = 351.4m s-1
Conceptual Questions
1. A spring which in initially in un-stretched condition, is first stretched by a length x and again by a further length x. The work done in the first case W1 is one third of the work done in second case W2. True or false?
Answer

2. Which is conserved in inelastic collision? Total energy (or) Kinetic energy?
Answer
Total energy is always conserved.
But K.E. is not conserved.
3. Is there any net work done by external forces on a car moving with a constant speed along a straight road?
Answer
No.
If a car is moving at a constant speed, then external force will be zero.
Because a = [v - u] / t
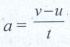
For constant speed v = u, then a=0. (a-acceleration)
F = ma .'. F = zero. i.e.. no external force.
W = F.S. = 0. So net work done is zero.
4. A car starts from rest and moves on a surface with uniform acceleration.
Draw the graph of kinetic energy versus displacement. What information you can get from that graph?
Answer

5. A charged particle moves towards another charged particle. Under what conditions the total momentum and the total energy of the system conserved?
Answer
(i) Both charged particles shall be dissimilar charge, (i.e. positive and negative)
(ii) After collision the charged particles; stick together permanent.
(iii) They should move with common velocity
Related Topics