Work, Energy and Power | Physics - Solved Example Problems | 11th Physics : UNIT 4 : Work, Energy and Power
Chapter: 11th Physics : UNIT 4 : Work, Energy and Power
Solved Example Problems
Work, Energy and Power | Physics
SOLVED EXAMPLE

2. A particle moves along X- axis from x=0 to x=8 under the influence of a force given by F= 3x 2 - 4x + 5. Find the work done in the process.
Solution:

3. A body of mass 10kg at rest is subjected to a force of 16N. Find the kinetic energy at the end of 10 s.
Solution:
Mass m = 10 kg
Force F = 16 N
time t = 10 s
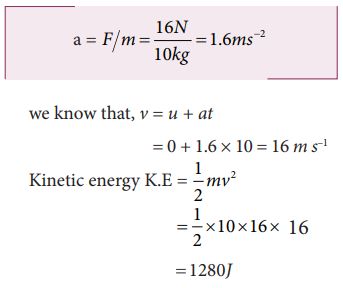
4. A body of mass 5kg is thrown up vertically with a kinetic energy of 1000 J. If acceleration due to gravity is 10ms-2, find the height at which the kinetic energy becomes half of the original value.
Solution:
Mass m = 5kg
K.E E = 1000J
g = 10m s-2
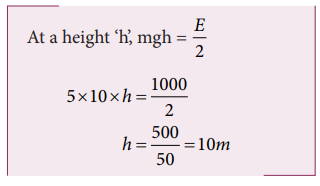
5. Two bodies of mass 60 kg and 30 kg move in the same direction along straight line with velocity 40 cm s-1 and 30 cm s-1 respectively suffer one dimensional elastic collision. Find their velocities after collision.
Solution:
Mass m1 = 60 kg
Mass m2 = 30 kg
V1 = 40cm s-1
V2 = 30cm s-1

Likewise,
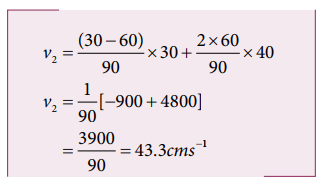
6. A particle of mass 70 g moving at 50 cm s-1 is acted upon by a variable force as shown in the figure. What will be its speed once the force stops?
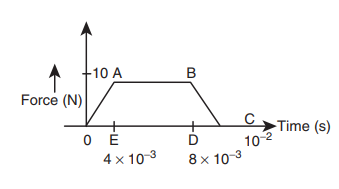
Solution:
The area under the graph gives the impulse.
Impulse I = area of ∆OAE+ area of rectangle ABDE+ area of ∆DBC
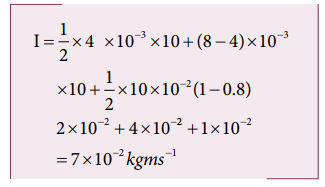
But Impulse = 2 × initial momentum of the particle= 2 × m × u
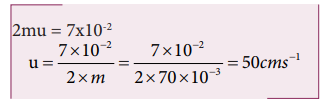
Hence the particle will reverse its direction and move with its initial speed.
7. A particle strikes a horizontal frictionless floor with a speed u at an angle θ with the vertical and rebounds with the speed v at an angleΦ with an vertical. The coefficient of restitution between the particle and floor is e. What is the magnitude of v?

Solution:
Applying component of velocities,
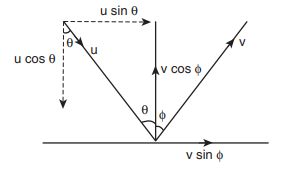
The x - component of velocity is
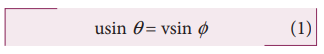
The magnitude of y – component of velocity is not same, therefore, using coefficient of restitution,

8. A particle of mass m is fixed to one end of a light spring of force constant k and un-stretched length l. It is rotated with an angular velocity ω in horizontal circle. What will be the length increase in the spring?
Solution:
Mass spring = m Force
constant = k
Un-stretched length = l
Angular velocity = ω
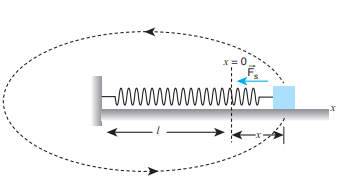
Let ‘x’ be the increase in the length of the spring.
The new length = (l+x) = r
When the spring is rotated in a horizontal circle,
Spring force = centripetal force.

9. A gun fires 8 bullets per second into a target X. If the mass of each bullet is 3 g and its speed 600 s-1. Then, calculate the power delivered by the bullets.
Solution:
Power = work done per second = total kinetic energy of 8 bullets per second
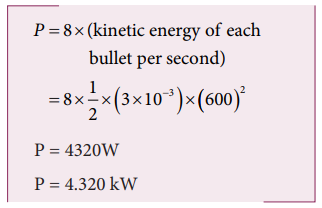
Solved Example Problems for Work
Example 4.1
A box is pulled with a force of 25 N to produce a displacement of 15 m. If the angle between the force and displacement is 30o, find the work done by the force.
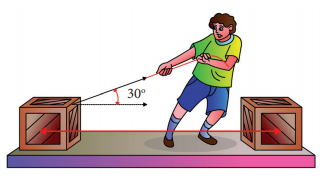
A box is pulled with a force of 25 N to produce a displacement of 15 m. If the angle between the force and displacement is 30o, find the work done by the force.

Solution
Force, F = 25 N
Displacement, dr = 15 m
Angle between F and dr, θ = 30o
Work done, W = Fdr cosθ
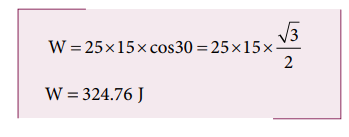
Force, F = 25 N
Displacement, dr = 15 m
Angle between F and dr, θ = 30o
Work done, W = Fdr cosθ
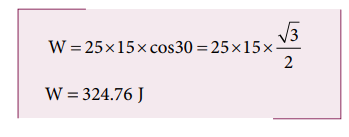
Solved Example Problems for Work done by a constant force
Example 4.2
An object of mass 2 kg falls from a height of 5 m to the ground. What is the work done by the gravitational force on the object? (Neglect air resistance; Take g = 10 m s-2)
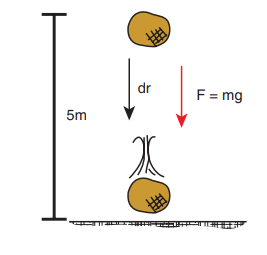
Example 4.2
An object of mass 2 kg falls from a height of 5 m to the ground. What is the work done by the gravitational force on the object? (Neglect air resistance; Take g = 10 m s-2)

Solution
In this case the force acting on the object is downward gravitational force 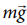 . This is a constant force.
. This is a constant force.
Work done by gravitational force is
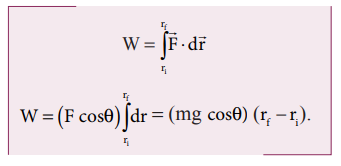
The object also moves downward which is in the direction of gravitational force (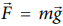 ) as shown in figure. Hence, the angle between them is θ = 0° cos0° = 1 and the displacement, (rf - r1) = 5m
) as shown in figure. Hence, the angle between them is θ = 0° cos0° = 1 and the displacement, (rf - r1) = 5m
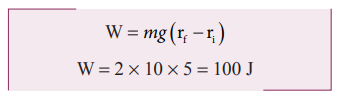
The work done by the gravitational force on the object is positive.
Example 4.3
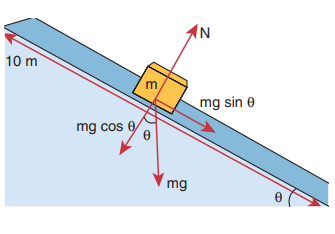
An object of mass m=1 kg is sliding from top to bottom in the frictionless inclined plane of inclination angle θ = 30o and the length of inclined plane is 10 m as shown in the figure. Calculate the work done by gravitational force and normal force on the object. Assume acceleration due to gravity, g = 10 m s-2
In this case the force acting on the object is downward gravitational force ![]() . This is a constant force.
. This is a constant force.
Work done by gravitational force is
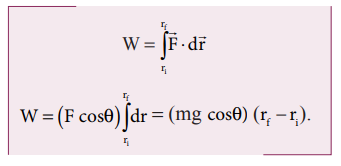
The object also moves downward which is in the direction of gravitational force (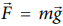 ) as shown in figure. Hence, the angle between them is θ = 0° cos0° = 1 and the displacement, (rf - r1) = 5m
) as shown in figure. Hence, the angle between them is θ = 0° cos0° = 1 and the displacement, (rf - r1) = 5m
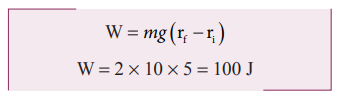
The work done by the gravitational force on the object is positive.
Example 4.3
An object of mass m=1 kg is sliding from top to bottom in the frictionless inclined plane of inclination angle θ = 30o and the length of inclined plane is 10 m as shown in the figure. Calculate the work done by gravitational force and normal force on the object. Assume acceleration due to gravity, g = 10 m s-2

Solution
We calculated in the previous chapter that the acceleration experienced by the object in the inclined plane as g sinθ .
According to Newton’s second law, the force acting on the mass along the inclined plane F = mg sinθ. Note that this force is constant throughout the motion of the mass.
The work done by the parallel component of gravitational force ( mg sinθ ) is given by
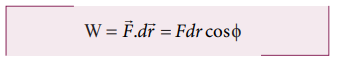
where ϕ is the angle between the force (mg sin θ) and the direction of motion (dr). In this case, force (mg sin θ) and the displacement (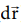 ) are in the same direction. Hence ϕ = o and cos ϕ = 1
) are in the same direction. Hence ϕ = o and cos ϕ = 1
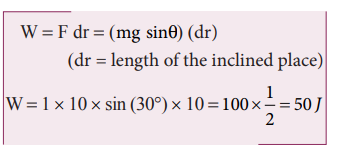
We calculated in the previous chapter that the acceleration experienced by the object in the inclined plane as g sinθ .
According to Newton’s second law, the force acting on the mass along the inclined plane F = mg sinθ. Note that this force is constant throughout the motion of the mass.
The work done by the parallel component of gravitational force ( mg sinθ ) is given by
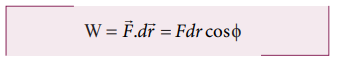
where ϕ is the angle between the force (mg sin θ) and the direction of motion (dr). In this case, force (mg sin θ) and the displacement (![]() ) are in the same direction. Hence ϕ = o and cos ϕ = 1
) are in the same direction. Hence ϕ = o and cos ϕ = 1
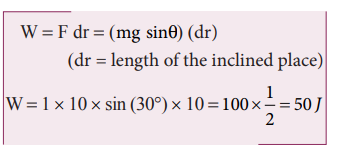
Example 4.4
If an object of mass 2 kg is thrown up from the ground reaches a height of 5 m and falls back to the Earth (neglect the air resistance). Calculate
a) The work done by gravity when the object reaches 5 m height
b) The work done by gravity when the object comes back to Earth
c) Total work done by gravity both in upward and downward motion and mention the physical significance of the result.
If an object of mass 2 kg is thrown up from the ground reaches a height of 5 m and falls back to the Earth (neglect the air resistance). Calculate
a) The work done by gravity when the object reaches 5 m height
b) The work done by gravity when the object comes back to Earth
c) Total work done by gravity both in upward and downward motion and mention the physical significance of the result.
Solution
When the object goes up, the displacement points in the upward direction whereas the gravitational force acting on the object points in downward direction. Therefore, the angle between gravitational force and displacement of the object is 180°.
a. The work done by gravitational force in the upward motion.
Given that ∆r =5 m and F mg
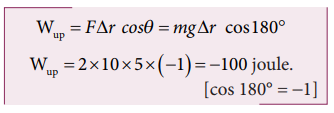
b. When the object falls back, both the gravitational force and displacement of the object are in the same direction. This implies that the angle between gravitational force and displacement of the object is 0°.
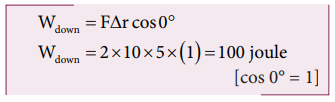
c. The total work done by gravity in the entire trip (upward and downward motion)
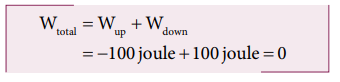
It implies that the gravity does not transfer any energy to the object. When the object is thrown upwards, the energy is transferred to the object by the external agency, which means that the object gains some energy. As soon as it comes back and hits the Earth, the energy gained by the object is transferred to the surface of the Earth (i.e., dissipated to the Earth).
When the object goes up, the displacement points in the upward direction whereas the gravitational force acting on the object points in downward direction. Therefore, the angle between gravitational force and displacement of the object is 180°.
a. The work done by gravitational force in the upward motion.
Given that ∆r =5 m and F mg
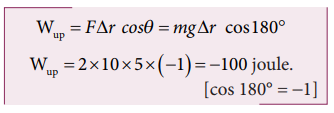
b. When the object falls back, both the gravitational force and displacement of the object are in the same direction. This implies that the angle between gravitational force and displacement of the object is 0°.
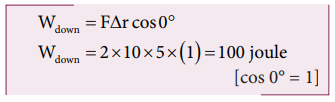
c. The total work done by gravity in the entire trip (upward and downward motion)
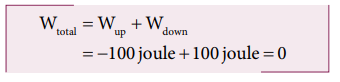
It implies that the gravity does not transfer any energy to the object. When the object is thrown upwards, the energy is transferred to the object by the external agency, which means that the object gains some energy. As soon as it comes back and hits the Earth, the energy gained by the object is transferred to the surface of the Earth (i.e., dissipated to the Earth).
Example 4.5
A weight lifter lifts a mass of 250 kg with a force 5000 N to the height of 5 m.
a. What is the workdone by the weight lifter?
b. What is the workdone by the gravity?
c. What is the net workdone on the object?
A weight lifter lifts a mass of 250 kg with a force 5000 N to the height of 5 m.
a. What is the workdone by the weight lifter?
b. What is the workdone by the gravity?
c. What is the net workdone on the object?
Solution
a. When the weight lifter lifts the mass, force and displacement are in the same direction, which means that the angle between them θ = 00. Therefore, the work done by the weight lifter,
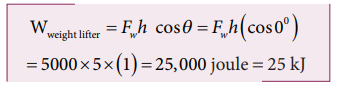
b. When the weight lifter lifts the mass, the gravity acts downwards which means that the force and displacement are in opposite direction. Therefore, the angle between them θ = 1800
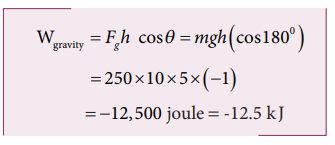
c. The net workdone (or total work done) on the object

a. When the weight lifter lifts the mass, force and displacement are in the same direction, which means that the angle between them θ = 00. Therefore, the work done by the weight lifter,
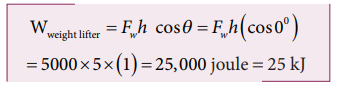
b. When the weight lifter lifts the mass, the gravity acts downwards which means that the force and displacement are in opposite direction. Therefore, the angle between them θ = 1800
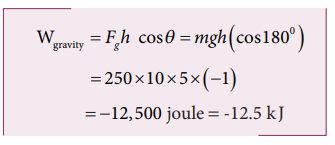
c. The net workdone (or total work done) on the object

Solved Example Problems for Work done by a variable force
Example 4.6
A variable force F = kx2 acts on a particle which is initially at rest. Calculate the work done by the force during the displacement of the particle from x = 0 m to x = 4 m. (Assume the constant k =1 N m-2)
A variable force F = kx2 acts on a particle which is initially at rest. Calculate the work done by the force during the displacement of the particle from x = 0 m to x = 4 m. (Assume the constant k =1 N m-2)
Solution
Work done,
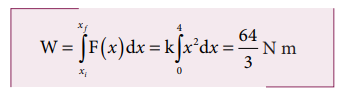
Work done,
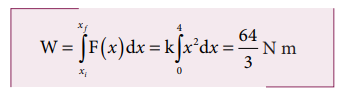
Solved Example Problems for Kinetic energy
Example 4.7
Two objects of masses 2 kg and 4 kg are moving with the same momentum of 20 kg m s-1.
a. Will they have same kinetic energy?
b. Will they have same speed?
Two objects of masses 2 kg and 4 kg are moving with the same momentum of 20 kg m s-1.
a. Will they have same kinetic energy?
b. Will they have same speed?
Solution
a. The kinetic energy of the mass is given by

Note that KE1 ≠ KE2 i.e., even though both are having the same momentum, the kinetic energy of both masses is not the same. The kinetic energy of the heavier object has lesser kinetic energy than smaller mass. It is because the kinetic energy is inversely proportional to the mass (KE ∝ 1/m) for a given momentum.
b. As the momentum, p = mv, the two objects will not have same speed.
a. The kinetic energy of the mass is given by

Note that KE1 ≠ KE2 i.e., even though both are having the same momentum, the kinetic energy of both masses is not the same. The kinetic energy of the heavier object has lesser kinetic energy than smaller mass. It is because the kinetic energy is inversely proportional to the mass (KE ∝ 1/m) for a given momentum.
b. As the momentum, p = mv, the two objects will not have same speed.
Solved Example Problems for Potential Energy
Example 4.8
An object of mass 2 kg is taken to a height 5 m from the ground g = 10ms-2 .
a. Calculate the potential energy stored in the object.
b. Where does this potential energy come from?
c. What external force must act to bring the mass to that height?
d. What is the net force that acts on the object while the object is taken to the height ‘h’?
An object of mass 2 kg is taken to a height 5 m from the ground g = 10ms-2 .
a. Calculate the potential energy stored in the object.
b. Where does this potential energy come from?
c. What external force must act to bring the mass to that height?
d. What is the net force that acts on the object while the object is taken to the height ‘h’?
Solution
a. The potential energy U =m g h = 2 × 10 × 5 = 100 J
Here the positive sign implies that the energy is stored on the mass.
b. This potential energy is transferred from external agency which applies the force on the mass.
c.

d. From the definition of potential energy, the object must be moved at constant velocity. So the net force acting on the object is zero.
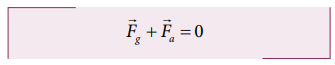
a. The potential energy U =m g h = 2 × 10 × 5 = 100 J
Here the positive sign implies that the energy is stored on the mass.
b. This potential energy is transferred from external agency which applies the force on the mass.
c.

d. From the definition of potential energy, the object must be moved at constant velocity. So the net force acting on the object is zero.
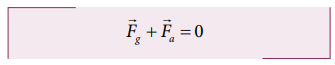
Solved Example Problems for Elastic Potential Energy
Example 4.9
Let the two springs A and B be such that kA>kB. On which spring will more work has to be done if they are stretched by the same force?
Example 4.9
Let the two springs A and B be such that kA>kB. On which spring will more work has to be done if they are stretched by the same force?
Solution
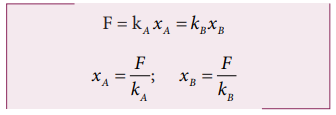
The work done on the springs are stored as potential energy in the springs.

kA>kB implies that UB>UA . Thus, more work is done on B than A.
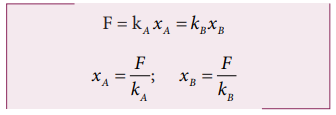
The work done on the springs are stored as potential energy in the springs.

kA>kB implies that UB>UA . Thus, more work is done on B than A.
Example 4.10
A body of mass m is attached to the spring which is elongated to 25 cm by an applied force from its equilibrium position.
a. Calculate the potential energy stored in the spring-mass system?
b. What is the work done by the spring force in this elongation?
c. Suppose the spring is compressed to the same 25 cm, calculate the potential energy stored and also the work done by the spring force during compression. (The spring constant, k = 0.1 N m-1).
A body of mass m is attached to the spring which is elongated to 25 cm by an applied force from its equilibrium position.
a. Calculate the potential energy stored in the spring-mass system?
b. What is the work done by the spring force in this elongation?
c. Suppose the spring is compressed to the same 25 cm, calculate the potential energy stored and also the work done by the spring force during compression. (The spring constant, k = 0.1 N m-1).
Solution
The spring constant, k = 0.1 N m-1
The displacement, x = 25 cm = 0.25 m
a. The potential energy stored in the spring is given by
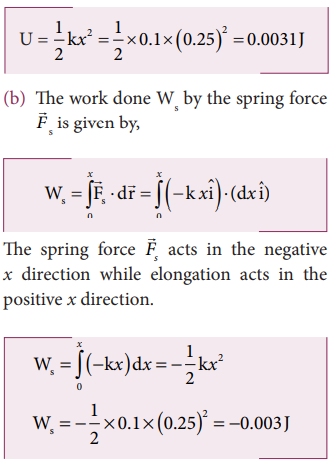
Note that the potential energy is defined through the work done by the external agency. The positive sign in the potential energy implies that the energy is transferred from the agency to the object. But the work done by the restoring force in this case is negative since restoring force is in the opposite direction to the displacement direction.
c. During compression also the potential energy stored in the object is the same.

Work done by the restoring spring force during compression is given by
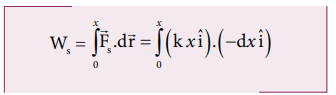
In the case of compression, the restoring spring force acts towards positive x-axis and displacement is along negative x direction.
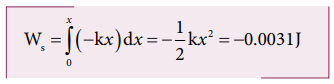
The spring constant, k = 0.1 N m-1
The displacement, x = 25 cm = 0.25 m
a. The potential energy stored in the spring is given by
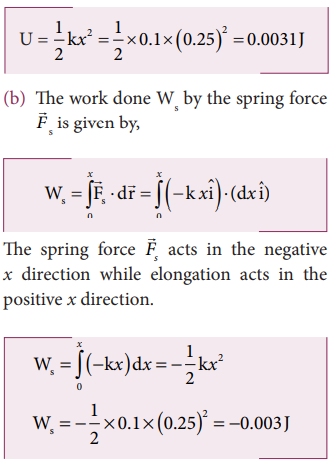
Note that the potential energy is defined through the work done by the external agency. The positive sign in the potential energy implies that the energy is transferred from the agency to the object. But the work done by the restoring force in this case is negative since restoring force is in the opposite direction to the displacement direction.
c. During compression also the potential energy stored in the object is the same.

Work done by the restoring spring force during compression is given by
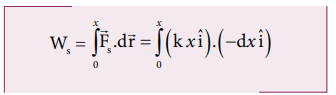
In the case of compression, the restoring spring force acts towards positive x-axis and displacement is along negative x direction.
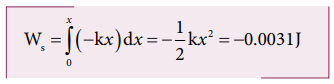
Solved Example Problems for Conservative and nonconservative forces
Example 4.11
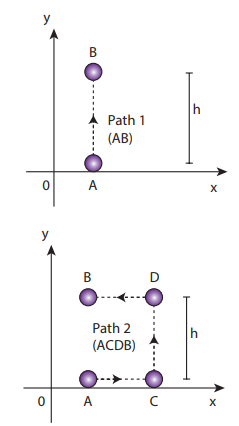
Compute the work done by the gravitational force for the following cases
Solution
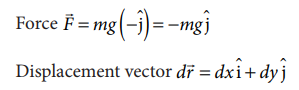
(As the displacement is in two dimension; unit vectors and are used)
a. Since the motion is only vertical, horizontal displacement component dx is zero. Hence, work done by the force along path 1 (of distance h).
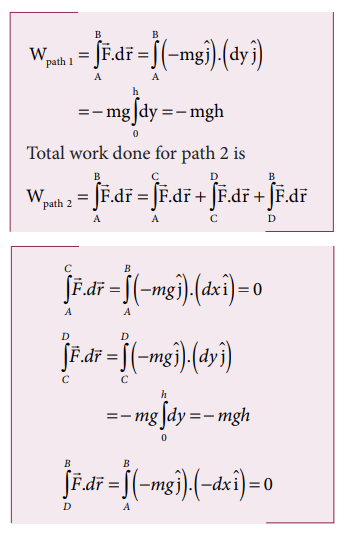
Therefore, the total work done by the force along the path 2 is
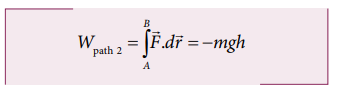
Note that the work done by the conservative force is independent of the path.
Compute the work done by the gravitational force for the following cases

Solution
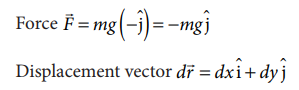
(As the displacement is in two dimension; unit vectors and are used)
a. Since the motion is only vertical, horizontal displacement component dx is zero. Hence, work done by the force along path 1 (of distance h).
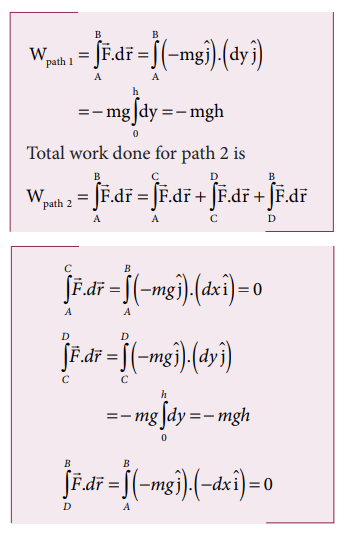
Therefore, the total work done by the force along the path 2 is
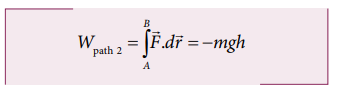
Note that the work done by the conservative force is independent of the path.
Example 4.12
Consider an object of mass 2 kg moved by an external force 20 N in a surface having coefficient of kinetic friction 0.9 to a distance 10 m. What is the work done by the external force and kinetic friction ? Comment on the result. (Assume g = 10 ms-2)
Solution
m = 2 kg, d = 10 m, Fext = 20 N, k = 0.9. When an object is in motion on the horizontal surface, it experiences two forces.
a. External force, Fext = 20 N
b. Kinetic friction,
fk =μkmg = 0.9x(2)x10=18N.
The work done by the external force Wext = Fs = 20x20 =200J
The work done by the force of kinetic friction Wk =fkd = (-18) x10=-180J Here the negative sign implies that the force of kinetic friction is pposite to the direction of displacement.
The total work done on the object
Wtotal = Wext + Wk = 200 J – 180 J = 20 J .
Since the friction is a non-conservative force, out of 200 J given by the external force, the 180 J is lost and it can not be recovered.
Consider an object of mass 2 kg moved by an external force 20 N in a surface having coefficient of kinetic friction 0.9 to a distance 10 m. What is the work done by the external force and kinetic friction ? Comment on the result. (Assume g = 10 ms-2)
Solution
m = 2 kg, d = 10 m, Fext = 20 N, k = 0.9. When an object is in motion on the horizontal surface, it experiences two forces.
a. External force, Fext = 20 N
b. Kinetic friction,
fk =μkmg = 0.9x(2)x10=18N.
The work done by the external force Wext = Fs = 20x20 =200J
The work done by the force of kinetic friction Wk =fkd = (-18) x10=-180J Here the negative sign implies that the force of kinetic friction is pposite to the direction of displacement.
The total work done on the object
Wtotal = Wext + Wk = 200 J – 180 J = 20 J .
Since the friction is a non-conservative force, out of 200 J given by the external force, the 180 J is lost and it can not be recovered.
Solved Example Problems for Law of conservation of energy
Example 4.13
An object of mass 1 kg is falling from the height h = 10 m. Calculate
a. The total energy of an object at h =10 m
b. Potential energy of the object when it is at h = 4 m
c. Kinetic energy of the object when it is at h = 4 m
d. What will be the speed of the object when it hits the ground?
(Assume g =10 m s-2)
An object of mass 1 kg is falling from the height h = 10 m. Calculate
a. The total energy of an object at h =10 m
b. Potential energy of the object when it is at h = 4 m
c. Kinetic energy of the object when it is at h = 4 m
d. What will be the speed of the object when it hits the ground?
(Assume g =10 m s-2)
Solution
a. The gravitational force is a conservative force. So the total energy remains constant throughout the motion. At h =10 m, the total energyE is entirely potential energy.
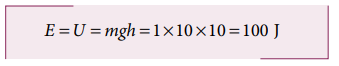
b. The potential energy of the object at h = 4 m is
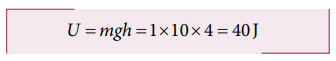
c. Since the total energy is constant throughout the motion, the kinetic energy at h = 4 m must be KE = E - U = 100 - 40 = 60J
Alternatively, the kinetic energy could also be found from velocity of the object at 4 m. At the height 4 m, the object has fallen through a height of 6 m.
The velocity after falling 6 m is calculated from the equation of motion,
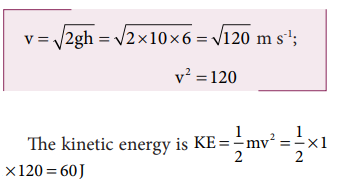
d. When the object is just about to hit the ground, the total energy is completely kinetic and the potential energy, U = 0.
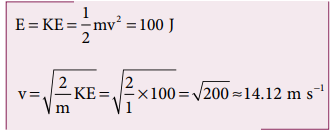
a. The gravitational force is a conservative force. So the total energy remains constant throughout the motion. At h =10 m, the total energyE is entirely potential energy.
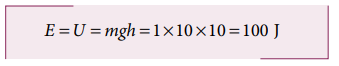
b. The potential energy of the object at h = 4 m is
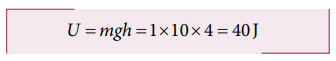
c. Since the total energy is constant throughout the motion, the kinetic energy at h = 4 m must be KE = E - U = 100 - 40 = 60J
Alternatively, the kinetic energy could also be found from velocity of the object at 4 m. At the height 4 m, the object has fallen through a height of 6 m.
The velocity after falling 6 m is calculated from the equation of motion,
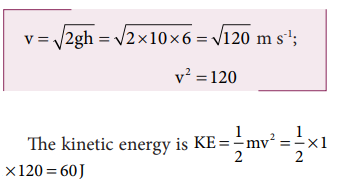
d. When the object is just about to hit the ground, the total energy is completely kinetic and the potential energy, U = 0.
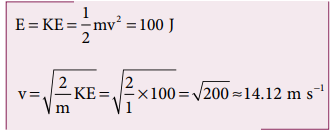
Example 4.14
A body of mass 100 kg is lifted to a height 10 m from the ground in two different ways as shown in the figure. What is the work done by the gravity in both the cases? Why is it easier to take the object through a ramp?
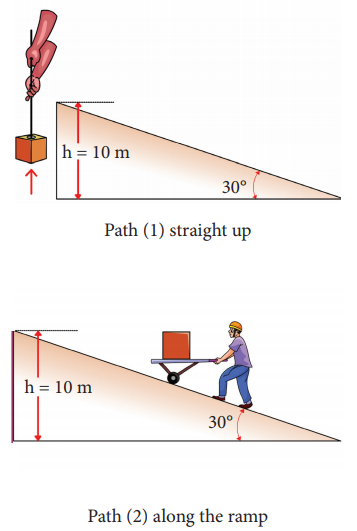
Solution
m = 100 kg, h = 10 m
Along path (1):
The minimum force F1 required to move the object to the height of 10 m should be equal to the gravitational force, F1 mg = 100 x 10 = 1000 N
The distance moved along path (1) is, =10 m
The work done on the object along path (1) is
W = Fh = 1000 x 10 = 10,000 J
Along path (2):
In the case of the ramp, the minimum force F2 that we apply on the object to take it up is not equal to mg, it is rather equal to mg sinθ .(mg sin < mg) .
Here, angle θ = 30o
Therefore, F2 = mg sinθ = 100 × 10 × sin30o = 100 × 10 × 0.5 = 500N
Hence, (mg sinθ < mg)
The path covered along the ramp is,
l = h/sin30 = 10/0.5 =20m
The work done on the object along path (2) is, W = F2 l = 500 × 20 = 10,000 J
Since the gravitational force is a conservative force, the work done by gravity on the object is independent of the path taken.
In both the paths the work done by the gravitational force is 10,000 J
Along path (1): more force needs to be applied against gravity to cover lesser distance .
Along path (2): lesser force needs to be applied against the gravity to cover more distance.
As the force needs to be applied along the ramp is less, it is easier to move the object along the ramp.
A body of mass 100 kg is lifted to a height 10 m from the ground in two different ways as shown in the figure. What is the work done by the gravity in both the cases? Why is it easier to take the object through a ramp?

Solution
m = 100 kg, h = 10 m
Along path (1):
The minimum force F1 required to move the object to the height of 10 m should be equal to the gravitational force, F1 mg = 100 x 10 = 1000 N
The distance moved along path (1) is, =10 m
The work done on the object along path (1) is
W = Fh = 1000 x 10 = 10,000 J
Along path (2):
In the case of the ramp, the minimum force F2 that we apply on the object to take it up is not equal to mg, it is rather equal to mg sinθ .(mg sin < mg) .
Here, angle θ = 30o
Therefore, F2 = mg sinθ = 100 × 10 × sin30o = 100 × 10 × 0.5 = 500N
Hence, (mg sinθ < mg)
The path covered along the ramp is,
l = h/sin30 = 10/0.5 =20m
The work done on the object along path (2) is, W = F2 l = 500 × 20 = 10,000 J
Since the gravitational force is a conservative force, the work done by gravity on the object is independent of the path taken.
In both the paths the work done by the gravitational force is 10,000 J
Along path (1): more force needs to be applied against gravity to cover lesser distance .
Along path (2): lesser force needs to be applied against the gravity to cover more distance.
As the force needs to be applied along the ramp is less, it is easier to move the object along the ramp.
Example 4.15
An object of mass m is projected from the ground with initial speed v0.
Find the speed at height h.
An object of mass m is projected from the ground with initial speed v0.
Find the speed at height h.
Solution
Since the gravitational force is conservative; the total energy is conserved throughout the motion.

Final values of potential energy, kinetic energy and total energy are measured at the height h.
By law of conservation of energy, the initial and final total energies are the same.
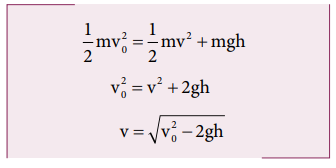
Note that in section (2.11.2) similar result is obtained using kinematic equation based on calculus method. However, calculation through energy conservation method is much easier than calculus method.
Since the gravitational force is conservative; the total energy is conserved throughout the motion.

Final values of potential energy, kinetic energy and total energy are measured at the height h.
By law of conservation of energy, the initial and final total energies are the same.
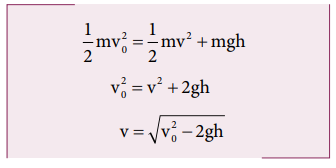
Note that in section (2.11.2) similar result is obtained using kinematic equation based on calculus method. However, calculation through energy conservation method is much easier than calculus method.
Example 4.16
An object of mass 2 kg attached to a spring is moved to a distance x =10 m from its equilibrium position. The spring constant k =1 N m-1and assume that the surface is frictionless.
a. When the mass crosses the equilibrium position, what is the speed of the mass?
b. What is the force that acts on the object when the mass crosses the equilibrium position and extremum position x = ± 10 m.
An object of mass 2 kg attached to a spring is moved to a distance x =10 m from its equilibrium position. The spring constant k =1 N m-1and assume that the surface is frictionless.
a. When the mass crosses the equilibrium position, what is the speed of the mass?
b. What is the force that acts on the object when the mass crosses the equilibrium position and extremum position x = ± 10 m.
Solution
a. Since the spring force is a conservative force, the total energy is constant. At x =10 m, the total energy is purely potential.
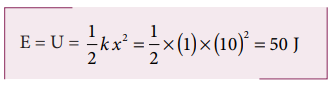
When the mass crosses the equilibrium position x = 0 , the potential energy
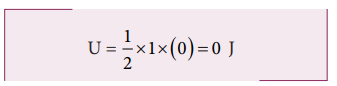
The entire energy is purely kinetic energy at this position.
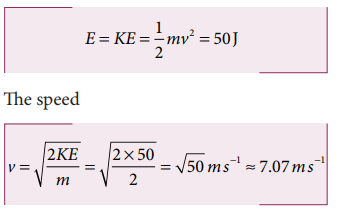
b. Since the restoring spring force is F = - kx, when the object crosses the equilibrium position, it experiences no force. Note that at equilibrium position, the object moves very fast. When the object is at x = +10 m (elongation), the force F = - k x
F = - (1) (10) = - 10 N. Here the negative sign implies that the force is towards equilibrium i.e., towards negative x-axis and when the object is at x = - 10 (compression), it experiences a forces F = - (1) (- 10) = +10 N. Here the positive sign implies that the force points towards positive x-axis.
The object comes to momentary rest at x = ±10m even though it experiences a maximum force at both these points.
a. Since the spring force is a conservative force, the total energy is constant. At x =10 m, the total energy is purely potential.
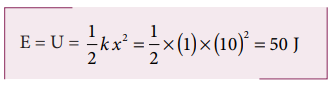
When the mass crosses the equilibrium position x = 0 , the potential energy
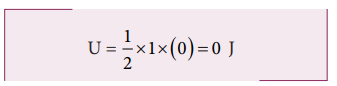
The entire energy is purely kinetic energy at this position.
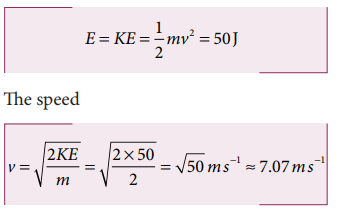
b. Since the restoring spring force is F = - kx, when the object crosses the equilibrium position, it experiences no force. Note that at equilibrium position, the object moves very fast. When the object is at x = +10 m (elongation), the force F = - k x
F = - (1) (10) = - 10 N. Here the negative sign implies that the force is towards equilibrium i.e., towards negative x-axis and when the object is at x = - 10 (compression), it experiences a forces F = - (1) (- 10) = +10 N. Here the positive sign implies that the force points towards positive x-axis.
The object comes to momentary rest at x = ±10m even though it experiences a maximum force at both these points.
Solved Example Problems for Motion in a vertical circle
Example 4.17
Water in a bucket tied with rope is whirled around in a vertical circle of radius 0.5 m. Calculate the minimum velocity at the lowest point so that the water does not spill from it in the course of motion. (g = 10 ms-2)
Water in a bucket tied with rope is whirled around in a vertical circle of radius 0.5 m. Calculate the minimum velocity at the lowest point so that the water does not spill from it in the course of motion. (g = 10 ms-2)
Solution

Solved Example Problems for Unit of power
Example 4.18
Calculate the energy consumed in electrical units when a 75 W fan is used for 8 hours daily for one month (30 days).
Calculate the energy consumed in electrical units when a 75 W fan is used for 8 hours daily for one month (30 days).
Solution
Power, P = 75 W
Time of usage, t = 8 hour × 30 days = 240 hours
Electrical energy consumed is the product of power and time of usage.
Electrical energy = power × time of usage = P × t

Power, P = 75 W
Time of usage, t = 8 hour × 30 days = 240 hours
Electrical energy consumed is the product of power and time of usage.
Electrical energy = power × time of usage = P × t

Solved Example Problems for Relation between power and velocity
Example 4.19
A vehicle of mass 1250 kg is driven with an acceleration 0.2 ms-2 along a straight level road against an external resistive force 500 N.Calculate the power delivered by the vehicle’s engine if the velocity of the vehicle is 30 m s-1 .
A vehicle of mass 1250 kg is driven with an acceleration 0.2 ms-2 along a straight level road against an external resistive force 500 N.Calculate the power delivered by the vehicle’s engine if the velocity of the vehicle is 30 m s-1 .
Solution
The vehicle’s engine has to do work against resistive force and make vechile to move with an acceleration. Therefore, power delivered by the vehicle engine is
Solved Example Problems for collision
The vehicle’s engine has to do work against resistive force and make vechile to move with an acceleration. Therefore, power delivered by the vehicle engine is
Solved Example Problems for collision
Solved Example Problems for Elastic collisions in one dimension
Example 4.20
A lighter particle moving with a speed of 10 m s-1 collides with an object of double its mass moving in the same direction with half its speed. Assume that the collision is a one dimensional elastic collision. What will be the speed of both particles after the collision?
A lighter particle moving with a speed of 10 m s-1 collides with an object of double its mass moving in the same direction with half its speed. Assume that the collision is a one dimensional elastic collision. What will be the speed of both particles after the collision?
Solution
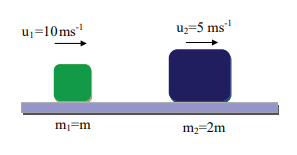
Let the mass of the fi rst body be m which moves with an initial velocity, u1 = 10 m s-1.
Therefore, the mass of second body is 2m and its initial velocity is u2 = ½ u1 = ½(10ms-1)
Then, the fi nal velocities of the bodies can be calculated from the equation (4.53) and equation (4.54)
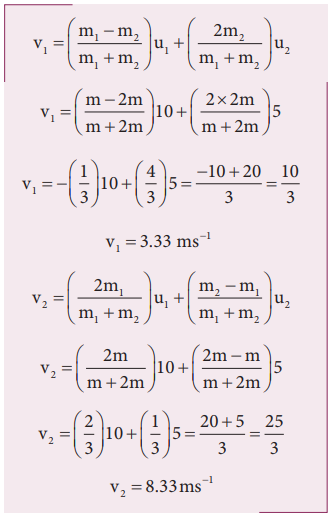
As the two speeds v1and v2 are positive, they move in the same direction with the velocities, 3.33 m s−1 and 8.33 m s−1 respectively.

Let the mass of the fi rst body be m which moves with an initial velocity, u1 = 10 m s-1.
Therefore, the mass of second body is 2m and its initial velocity is u2 = ½ u1 = ½(10ms-1)
Then, the fi nal velocities of the bodies can be calculated from the equation (4.53) and equation (4.54)
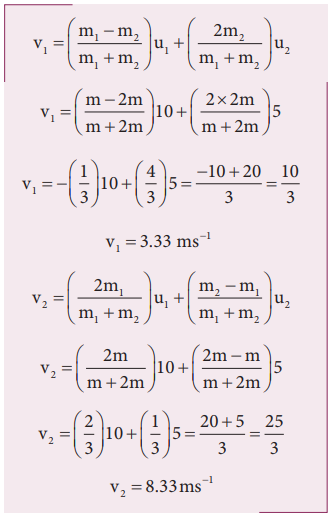
As the two speeds v1and v2 are positive, they move in the same direction with the velocities, 3.33 m s−1 and 8.33 m s−1 respectively.
Solved Example Problems for Perfect inelastic collision
Example 4.21
A bullet of mass 50 g is fired from below into a suspended object of mass 450 g. The object rises through a height of 1.8 m with bullet remaining inside the object. Find the speed of the bullet. Take g = 10 ms-2.
A bullet of mass 50 g is fired from below into a suspended object of mass 450 g. The object rises through a height of 1.8 m with bullet remaining inside the object. Find the speed of the bullet. Take g = 10 ms-2.
Solution
m1 = 50 g = 0.05 kg; m2 = 450 g = 0.45kg
The speed of the bullet is u1. The second body is at rest u2 = 0 . Let the common velocity of the bullet and the object after the bullet is embedded into the object is v.
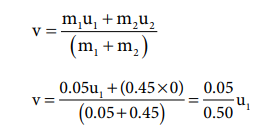
The combined velocity is the initial velocity for the vertical upward motion of the combined bullet and the object. From second equation of motion,
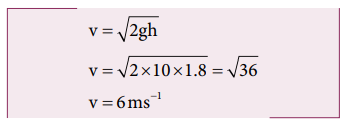
Substituting this in the above equation, the value of u1 is
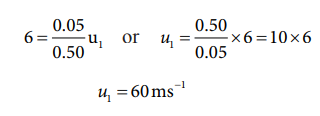
m1 = 50 g = 0.05 kg; m2 = 450 g = 0.45kg

The speed of the bullet is u1. The second body is at rest u2 = 0 . Let the common velocity of the bullet and the object after the bullet is embedded into the object is v.
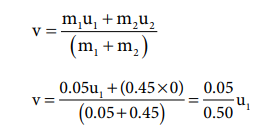
The combined velocity is the initial velocity for the vertical upward motion of the combined bullet and the object. From second equation of motion,
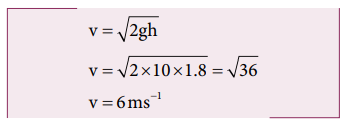
Substituting this in the above equation, the value of u1 is
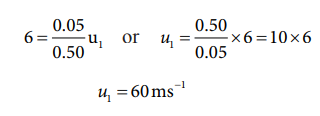
Solved Example Problems for Coefficient of restitution (e)
Example 4.22
Show that the ratio of velocities of equal masses in an inelastic collision when one of the masses is stationary is
v1/v2 = 1-e/1+e
Show that the ratio of velocities of equal masses in an inelastic collision when one of the masses is stationary is
v1/v2 = 1-e/1+e
Solution
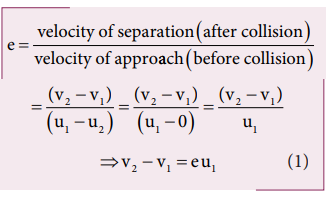
From the law of conservation of linear momentum,
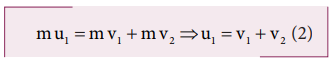
Using the equation (2) for u1 in (1), we get

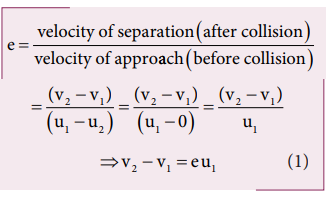
From the law of conservation of linear momentum,
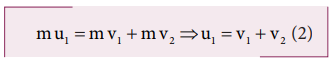
Using the equation (2) for u1 in (1), we get

Work, Energy and Power | Physics
Numerical Problems
1. Calculate the work done by a force of 30 N in lifting a load of 2kg to a height of 10m (g = 10ms-2)
Answer:
Given :
Force mg = 30 N ; height = 10 m
Work done to lift a load W = ?
W = F.S (or) mgh
= 30x10
W = 300 J
Ans: 300J
2. A ball with a velocity of 5 m s-1 impinges at angle of 60˚ with the vertical on a smooth horizontal plane. If the coefficient of restitution is 0.5, find the velocity and direction after the impact.
Answer
The impluse on the ball acts perpendicular to the smooth plane.

(i) The component of velocity of ball parallel to the surface.
(ii) For the component of velocity of ball perpendicular to the surface, apply law of restitution.
The component of velocity parallel to the surface will be changed.
v cos α = u cos 60°
v cos α = 5 × 1/2 = 5/2 ….(1)
According to law of restitution
v sin α = e u sin 60°
v sin α = 1/2 × 5 × √3/2 = 5 (√3/4) ….(2)
Squaring and adding (1) and (2)
v2 (sin2α + cos2α) =
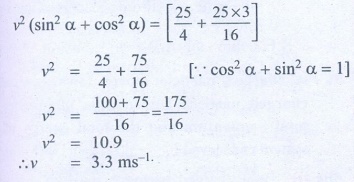
v = 3.3 ms-1
Ans: v = 0.3 m s-1
3. A bob of mass m is attached to one end of the rod of negligible mass and length r, the other end of which is pivoted freely at a fixed center O as shown in the figure. What initial speed must be given to the object to reach the top of the circle? (Hint: Use law of conservation of energy). Is this speed less or greater than speed obtained in the section 4.2.9 ?
Ans: √4gr ms

Answer
The horizontal distance, draw the point of projection to the point where the ball returns to the same level
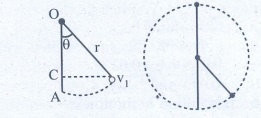
AC = OA-OC = r - rcosθ
minimum velocity = at vL = √[5gr]
v12 = vL2 - 2gr (1 - cos θ)
v12 = 5gr - 2gr (l-cosθ)
If θ = 60°
v12 = 5gr-2gr(l – 1/2)
v12 = 5gr - gr => v12 = 4gr
v1 = √[4gr] ms-1.
4. Two different unknown masses A and B collide. A is initially at rest when B has a speed v. After collision B has a speed v/2 and moves at right angles to its original direction of motion. Find the direction in which A moves after collision.
Answer:
Momentium is censerved in both × and y direction.
In x - direction
MBVB = O + MAVA' cosɸ ...(l)
In y - direction
O = MBVB' - MAVA'sinɸ ...(2)
(2)/(1) tanɸ = VB’/VB = 1/2
tan ɸ = ½
ɸ = 26.6° (or) 26° 36' [1° = 60']
Ans: θ = 26° 33′
5. A bullet of mass 20 g strikes a pendulum of mass 5 kg. The centre of mass of pendulum rises a vertical distance of 10 cm. If the bullet gets embedded into the pendulum, calculate its initial speed.
Answer
Mass of the bullet m1 = 20 g = 0.02 kg.
Mass of the pendulum m2 = 5 kg
Centre of mass of pendulum rises to a height = h = 10 cm = 0.1 m
Speed of the bullet = u1
Pendulum is at rest .:. u2 = 0
Common velocity of the bullet and the pendulum after the bullet is embeded into the object = v
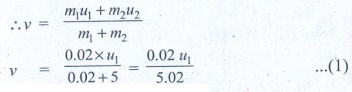
From II equation of motion
v = √[2gh] = √[2x9.8x0.1] = √[1.96] = 1.4 ms-1
Substitute the value of v in equation (1)
1.4 = 0.02 u1/5.02
u1 = 5.02x1.4 / 0.02
u1 = 351.4 ms-1
Ans: v = 351.4m s-1
Related Topics