Solved Example Problems for Law of conservation of energy

Solved Example Problems for Law of conservation of energy

Example 4.13

An object of mass 1 kg is falling from the height h = 10 m. Calculate

a. The total energy of an object at h =10 m

b. Potential energy of the object when it is at h = 4 m

c. Kinetic energy of the object when it is at h = 4 m

d. What will be the speed of the object when it hits the ground?

(Assume g =10 m s-2)

Solution

a. The gravitational force is a conservative force. So the total energy remains constant throughout the motion. At h =10 m, the total energyE is entirely potential energy.

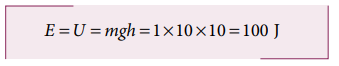
b. The potential energy of the object at h = 4 m is

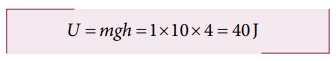
c. Since the total energy is constant throughout the motion, the kinetic energy at h = 4 m must be KE = E - U = 100 - 40 = 60J

Alternatively, the kinetic energy could also be found from velocity of the object at 4 m. At the height 4 m, the object has fallen through a height of 6 m.

The velocity after falling 6 m is calculated from the equation of motion,

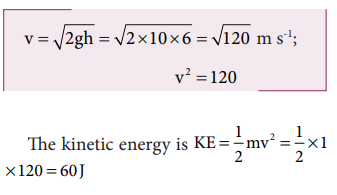
d. When the object is just about to hit the ground, the total energy is completely kinetic and the potential energy, U = 0.

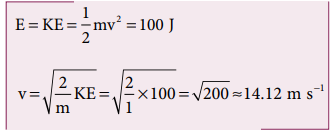
Example 4.14

A body of mass 100 kg is lifted to a height 10 m from the ground in two different ways as shown in the figure. What is the work done by the gravity in both the cases? Why is it easier to take the object through a ramp?

Solution

m = 100 kg, h = 10 m

Along path (1):

The minimum force F1 required to move the object to the height of 10 m should be equal to the gravitational force, F1 mg = 100 x 10 = 1000 N

The distance moved along path (1) is, =10 m

The work done on the object along path (1) is

W = Fh = 1000 x 10 = 10,000 J

Along path (2):

In the case of the ramp, the minimum force F2 that we apply on the object to take it up is not equal to mg, it is rather equal to mg sinθ .(mg sin < mg) .

Here, angle θ = 30o

Therefore, F2  = mg sinθ = 100 × 10 ×  sin30o = 100 × 10 × 0.5 = 500N

Hence,  (mg sinθ < mg)

The path covered along the ramp is,

l = h/sin30 = 10/0.5 =20m

The work done on the object along path  (2) is, W = F2 l = 500 × 20 = 10,000 J

Since the gravitational force is a conservative force, the work done by gravity on the object is independent of the path taken.

In both the paths the work done by the gravitational force is 10,000 J

Along path (1): more force needs to be applied against gravity to cover lesser distance .

Along path (2): lesser force needs to be applied against the gravity to cover more distance.

As the force needs to be applied along the ramp is less, it is easier to move the object along the ramp.

Example 4.15

An object of mass m is projected from the ground with initial speed v0.

Find the speed at height h.

Solution

Since the gravitational force is conservative; the total energy is conserved throughout the motion.

Final values of potential energy, kinetic energy and total energy are measured at the height h.

By law of conservation of energy, the initial and final total energies are the same.

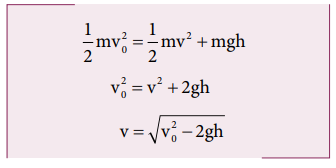
Note that in section (2.11.2) similar result is obtained using kinematic equation based on calculus method. However, calculation through energy conservation method is much easier than calculus method.

Example 4.16

An object of mass 2 kg attached to a spring is moved to a distance x =10 m from its equilibrium position. The spring constant k =1 N m-1and assume that the surface is frictionless.

a. When the mass crosses the equilibrium position, what is the speed of the mass?

b. What is the force that acts on the object when the mass crosses the equilibrium position and extremum position x = ± 10 m.

Solution

a. Since the spring force is a conservative force, the total energy is constant. At x =10 m, the total energy is purely potential.

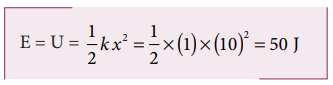
When the mass crosses the equilibrium position x = 0 , the potential energy

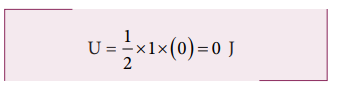
The entire energy is purely kinetic energy at this position.

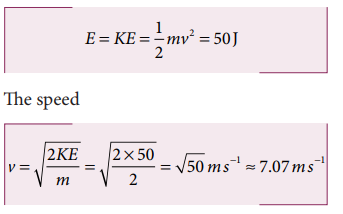
b. Since the restoring spring force is F = - kx, when the object crosses the equilibrium position, it experiences no force. Note that at equilibrium position, the object moves very fast. When the object is at x = +10 m (elongation), the force F = - k x

F = - (1) (10) = - 10 N. Here the negative sign implies that the force is towards equilibrium i.e., towards negative x-axis and when the object is at x = - 10 (compression), it experiences a forces F = - (1) (- 10) = +10 N. Here the positive sign implies that the force points towards positive x-axis.

The object comes to momentary rest at x = ±10m even though it experiences a maximum force at both these points.