Book Back Numerical Problems

1. Calculate the work done by a force of 30 N in lifting a load of 2kg to a height of 10m (g = 10ms-2)

Answer:

Given :

Force mg = 30 N ; height = 10 m

Work done to lift a load W = ?

W = F.S (or) mgh

= 30x10

W = 300 J 

Ans: 300J

2. A ball with a velocity of 5 m s-1 impinges at angle of 60˚ with the vertical on a smooth horizontal plane. If the coefficient of restitution is 0.5, find the velocity and direction after the impact.

Answer

The impluse on the ball acts perpendicular to the smooth plane.

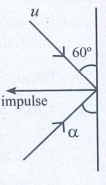
(i) The component of velocity of ball parallel to the surface.

(ii) For the component of velocity of ball perpendicular to the surface, apply law of restitution.

The component of velocity parallel to the surface will be changed.

v cos α = u cos 60°

v cos α = 5 × 1/2 = 5/2       ….(1)

According to law of restitution

v sin α = e u sin 60°

v sin α = 1/2 × 5 × √3/2 =  5 (√3/4)        ….(2)

Squaring and adding (1) and (2)

v2 (sin2α + cos2α) = 

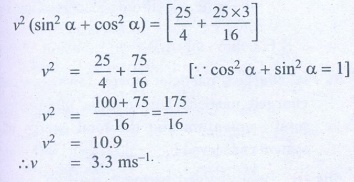
v = 3.3 ms-1

Ans: v = 0.3 m s-1

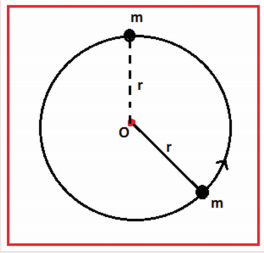
3. A bob of mass m is attached to one end of the rod of negligible mass and length r, the other end of which is pivoted freely at a fixed center O as shown in the figure. What initial speed must be given to the object to reach the top of the circle? (Hint: Use law of conservation of energy). Is this speed less or greater than speed obtained in the section 4.2.9 ?

Ans: √4gr ms^-1

Answer

The horizontal distance, draw the point of projection to the point where the ball returns to the same level

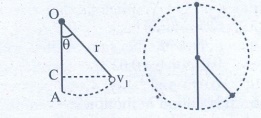
AC = OA-OC = r - rcosθ

minimum velocity = at vL = √[5gr]

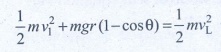
v12 = vL2 - 2gr (1 - cos θ)

v12 = 5gr - 2gr (l-cosθ)

If θ = 60°

v12 = 5gr-2gr(l – 1/2)

v12 = 5gr - gr => v12 = 4gr

v1 = √[4gr] ms-1.

4. Two different unknown masses A and B collide. A is initially at rest when B has a speed v. After collision B has a speed v/2 and moves at right angles to its original direction of motion. Find the direction in which A moves after collision.

Answer:

Momentium is censerved in both × and y direction.

In x - direction

MBVB = O + MAVA' cosɸ ...(l)

In y - direction

O = MBVB' - MAVA'sinɸ  ...(2)

(2)/(1) tanɸ = VB’/VB = 1/2

tan ɸ = ½

ɸ = 26.6° (or) 26° 36' [1° = 60']

Ans: θ = 26° 33′

5. A bullet of mass 20 g strikes a pendulum of mass 5 kg. The centre of mass of pendulum rises a vertical distance of 10 cm. If the bullet gets embedded into the pendulum, calculate its initial speed.

Answer

Mass of the bullet m1 = 20 g = 0.02 kg.

Mass of the pendulum m2 = 5 kg

Centre of mass of pendulum rises to a height = h = 10 cm = 0.1 m

Speed of the bullet = u1

Pendulum is at rest .:. u2 = 0

Common velocity of the bullet and the pendulum after the bullet is embeded into the object = v

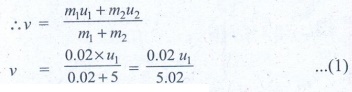
From II equation of motion

v = √[2gh] = √[2x9.8x0.1] = √[1.96] = 1.4 ms-1

Substitute the value of v in equation (1)

1.4 = 0.02 u1/5.02

u1 = 5.02x1.4 / 0.02

u1 = 351.4 ms-1

Ans: v = 351.4m s-1