Choose the correct answers

1. A uniform force of (2iˆ+ ˆj) N acts on a particle of mass 1 kg. The particle displaces from position (3  ˆj + ˆk ) m to (5iˆ­+3ˆj) m. The work done by the force on the particle is 

(a) 9 J

(b) 6 J

(c) 10 J

(d) 12 J

Answer: c) 10J

Solution:

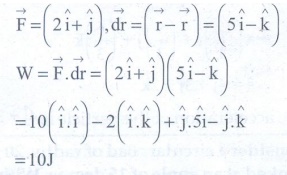
= 10J

2. A ball of mass 1 kg and another of mass 2 kg are dropped from a tall building whose height is 80 m. After, a fall of 40 m each towards Earth, their respective kinetic energies will be in the ratio of 

(a) √2 : 1

(b) 1 : √2

(c) 2 : 1

(d) 1 : 2

Answer: d) 1 : 2

Solution:

v_i = v₂ = v 40m

m₁ = 1kg

m₂ = 2kg

kE₁ / kE₂ = [ 1/2 m₁v² ] / [ 1/2 m₂v² ] = m₁ / m₂ = 1 / 2

∴kE₁ : kE₂ = 1 : 2

3. A body of mass 1 kg is thrown upwards with a velocity 20 m s−1. It momentarily comes to rest after attaining a height of 18 m. How much energy is lost due to air friction?. (Take g= 10ms-2 ) 

(a) 20 J

(b) 30 J

(c) 40 J

(d) 10 J

Answer: a) 20 J

Solution:

u = 20ms^-1

m = 1kg

KE = 1/2 mu²

 = 1/2 × 1 × 20 × 20

 = 200J

PE_max = mgh_max = 200J

PE₁ = mgh = 1 ×10 ×18=180J

energy lose = 200 − 180 = 20J

4. An engine pumps water continuously through a hose. Water leaves the hose with a velocity v and m is the mass per unit length of the water of the jet. What is the rate at which kinetic energy is imparted to water ?. 

a) ½ mv2

b) mv2

c) ½ mu2

d) mu2

Answer: a) 1/2 mv³

Solution:

Mass of water flowing per second = mv

Rate of K.E imparted = 1/2 mv³

= 1/2 (mv) × v²

= 1/2 mv × v² = 1/2 mv³

5. A body of mass 4 m is lying in xy-plane at rest. It suddenly explodes into three pieces. Two pieces each of mass m move perpendicular to each other with equal speed v. The total kinetic energy generated due to explosion is 

(a) mv2

(b) 3/2 mv2

(c) 2mv2

(d) 4mv2

Answer: b) 3/2 mv²

Solution: p_i = 0

∴ KE = 1/2 mv² + 1/2 mv² + 1/2 (2 m) v²

 = mv² + mv²/2 = 3/2 mv²

6. The potential energy of a system increases, if work is done 

(a) by the system against a conservative force

(b) by the system against a non-conservative force

(c) upon the system by a conservative force

(d) upon the system by a non-conservative force

Answer: a) by the system against a conservative force 

7. What is the minimum velocity with which a body of mass m must enter a vertical loop of radius R so that it can complete the loop?. 

(a) √(2gR)

(b) √(3gR)

(c) √(5gR)

(d) √(gR)

Answer: (c) √(5gR)

Solution:

Maximum velocity of the bottom of a vertical is √(5gR)

8. The work done by the conservative force for a closed path is 

(a) always negative

(b) zero

(c) always positive

(d) not defined

Answer: b) zero

9. If the linear momentum of the object is increased by 0.1%, then the kinetic energy is increased by 

(a) 0.1 %

(b) 0.2%

(c) 0.4%

(d) 0.01%

Answer: b) 0.2%

Solution:

kE_i = p² / 2m = k

p’ = 0.1% p = (1 + 0.001) p = 1.001p

KE_f = (p´)² / 2m = 1.002001 K

ΔKE = KE_f − KE_i

= 1.002K – K = 0.002K

ΔKE = 0.002 × 100 = 0.2%

10. If the potential energy of the particle is ­α - β/2 x2, then force experienced by the particle is 

(a) F=β/2 x2

(b) F=βx

(c) F=-βx

(d) F=-β/2 x2

Answer: b) F = βx

Solution :

u = α – (β/2)x²

F = -du / dx = -d/dx ( α – (1/2)β x² )

= 0 + [ 1/2 β (2x) ]

= βx

11. A wind-powered generator converts wind energy into electric energy. Assume that the generator converts a fixed fraction of the wind energy intercepted by its blades into electrical energy. For wind speed v, the electrical power output will be proportional to 

(a) v

(b) v2

(c) v3

(d) v4

Answer: c) v³

Solution:

Density of air = ρ

Cross section area of blades = A

Length of blades = x

Mass m = ρAX

KE = 1/2 mv² = 1/2 ρAXv²

t = x / v

Power P = KE / Δt =1/2 ρAXv² × v/x

= 1/2 ρAV³

12. Two equal masses m1 and m2 are moving along the same straight line with velocities 5ms-1 and -9ms-1 respectively. If the collision is elastic, then calculate the velocities after the collision of m1 and m2, respectively 

(a) -4ms-1 and 10 ms-1

(b) 10ms-1 and 0 ms-1

(c) -9ms-1 and 5 ms-1

(d) 5 ms-1 and 1 ms-1

Answer: c) -9 ms^-1 and 5 ms^-1

Solution:

For equal mass m₁ = m₂

∴v₁ = u₂ & v₂ = u₁

here u₁ = ms^-1; u₂ = −9ms^-1

∴v₁ = −9ms⁻¹; v₂ = 5ms⁻¹

13. A particle is placed at the origin and a force F=kx  is acting on it (where k is a positive constant). If U(0)=0, the graph of U(x­) versus x will be (where U is the potential energy function)

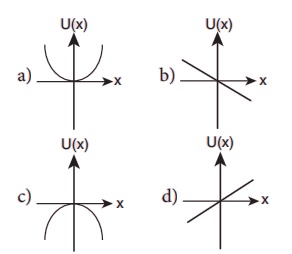
Answer: c) 

Solution:

u = − ^x∫₀ F.dx

 = − ^x∫₀ Kxdx

u = −K [ x² / 2 ]^x = − 1/2 Kx²

u(0) = 0; u = (x) = − Kx²

x² = −u (x)

14. A particle which is constrained to move along x-axis, is subjected to a force in the same direction which varies with the distance x of the particle from the origin as F(x) =-kx+ax3.

Here, k and a are positive constants. For x ≥ 0, the functional form of the potential energy U(x) of the particle is

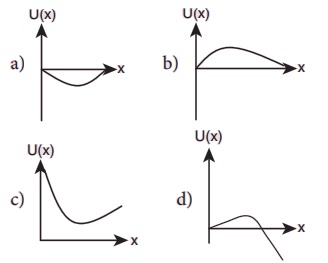
Answer: d) 

Solution:

du_x = −F.dx

u_x = −^x∫₀ Fdx = – [ (Kx²/2) + (ax⁴ / 4) ]

= (kx² / 2) – (ax⁴ / 4)

u = 0 at x = 0 & x = √( 2k / a )

x = 0, F = 0 but F = – du/dx

x = 0, du / dx = 0

15. A spring of force constant k is cut into two pieces such that one piece is double the length of the other. Then, the long piece will have a force constant of 

(a) 2/3 k

(b) 3/2 k

(c) 3k

(d) 6k

Answer: b) 3/2 k

Solution:

k ∝ 1 / l ;

 l₁ = l / 3

l₂ = 2l / 3

k = 1 / l₂ = 3 / 2l = (3/2) × (1/l) = 3/2 (k)

k = 3/2 k

Answers

1) c 2) d 3) a 4) a 5) b

6) a 7) c 8) b 9) b 10) c

11) c 12) c 13) c 14) d 15) b