Power

POWER

Definition of power

Power is a measure of how fast or slow a work is done. Power is defined as the rate of work done or energy delivered.

Average power

The average power (P_av) is defined as the ratio of the total work done to the total time taken.

Instantaneous power

The instantaneous power (P_inst) is defined as the power delivered at an instant (as time interval approaches zero),

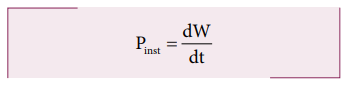
Unit of power

Power is a scalar quantity. Its dimension is [ML²T^-3]. The SI unit of power is watt (W), named after the inventor of the steam engine James Watt. One watt is defined as the power when one joule of work is done in one second, (1 W = 1 J s^-1).

The higher units are kilowatt(kW), megawatt(MW), and Gigawatt(GW).

1kW = 1000 W = 10³ watt

 1MW = 10⁶ watt

 1GW = 10⁹ watt

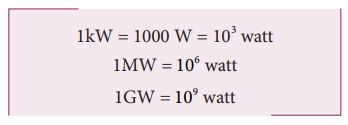
For motors, engines and some automobiles an old unit of power still commercially in use which is called as the horse-power (hp). We have a conversion for horse-power (hp) into watt (W) which is,

1 hp = 746 W

All electrical goods come with a definite power rating in watt printed on them. A 100 watt bulb consumes 100 joule of electrical energy in one second. The energy measured in joule in terms of power in watt and time in second is written as, 1 J =1 W s. When electrical appliances are put in use for long hours, they consume a large amount of energy. Measuring the electrical energy in a small unit watt. second (W s) leads to handling large numerical values. Hence, electrical energy is measured in the unit called kilowatt hour (kWh).

1 electrical unit = 1 kWh = 1 x (10³W) x (3600 s)

1 electrical unit = 3600×10³ Ws

1 electrical unit = 3.6×10⁶ J

1 kWh = 3.6×10⁶ J

Electricity bills are generated in units of kWh for electrical energy consumption. 1 unit of electrical energy is 1 kWh. (Note: kWh is unit of energy and not of power.)

Relation between power and velocity

The work done by a force  for a displacement d is

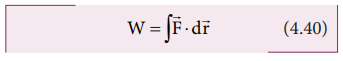
Left hand side of the equation (4.40) can be written as

Substituting equation (4.41) and equation (4.42) in equation (4.40), we get

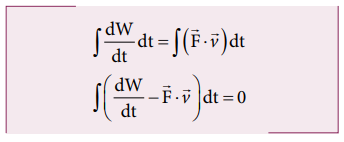
This relation is true for any arbitrary value of dt. This implies that the term within the bracket must be equal to zero, i.e.,

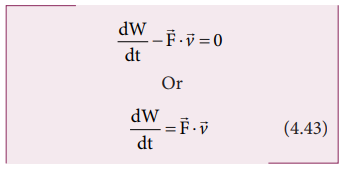
Solved Example Problems for Unit of power

Example 4.18

Calculate the energy consumed in electrical units when a 75 W fan is used for 8 hours daily for one month (30 days).

Solution

Power, P = 75 W

Time of usage, t = 8 hour × 30 days = 240 hours

Electrical energy consumed is the product of power and time of usage.

Electrical energy = power × time of usage = P × t

Solved Example Problems for Relation between power and velocity

Example 4.19

A vehicle of mass 1250 kg is driven with an acceleration 0.2 ms-2 along a straight level road against an external resistive force 500 N.Calculate the power delivered by the vehicle’s engine if the velocity of the vehicle is 30 m s-1 .

Solution

The vehicle’s engine has to do work against resistive force and make vechile to move with an acceleration. Therefore, power delivered by the vehicle engine is