Chapter: 11th Physics : UNIT 4 : Work, Energy and Power
Potential Energy
Potential Energy
The potential energy of a body is associated with its position and configuration with respect to its surroundings. This is because the various forces acting on the body also depends on position and configuration.
“Potential energy of an object at a point P is defined as the amount of work done by an external force in moving the object at constant velocity from the point O (initial location) to the point P (final location). At initial point O potential energy can be taken as zero.
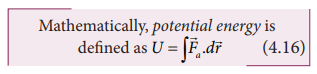
where the limit of integration ranges from initial location point O to final location point P.
We have various types of potential energies. Each type is associated with a particular force. For example,
(i) The energy possessed by the body due to gravitational force gives rise to gravitational potential energy.
(ii) The energy due to spring force and other similar forces give rise to elastic potential energy.
(iii) The energy due to electrostatic force on charges gives rise to electrostatic potential energy.
We will learn more about conservative forces in the section 4.2.7. Now, we continue to discuss more about gravitational potential energy and elastic potential energy.
Potential energy near the surface of the Earth
The gravitational potential energy (U) at some height h is equal to the amount of work required to take the object from ground to that height h with constant velocity.
Let us consider a body of mass m being moved from ground to the height h against the gravitational force as shown in Figure 4.8.
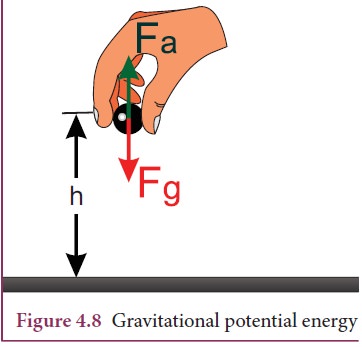
The gravitational force ![]() g acting on the body is,
g acting on the body is, ![]() g = - mg jˆ (as the force is in y direction, unit vector ˆj is used). Here, negative sign implies that the force is acting vertically downwards. In order to move the body without acceleration (or with constant velocity), an external applied force
g = - mg jˆ (as the force is in y direction, unit vector ˆj is used). Here, negative sign implies that the force is acting vertically downwards. In order to move the body without acceleration (or with constant velocity), an external applied force ![]() a equal in magnitude but opposite to that of gravitational force
a equal in magnitude but opposite to that of gravitational force ![]() g has to be applied on the body i.e.,
g has to be applied on the body i.e., ![]() a = -
a = - ![]() g . This implies that
g . This implies that ![]() a = + mg jˆ. The positive sign implies that the applied force is in vertically upward direction. Hence, when the body is lifted up its velocity remains unchanged and thus its kinetic energy also remains constant.
a = + mg jˆ. The positive sign implies that the applied force is in vertically upward direction. Hence, when the body is lifted up its velocity remains unchanged and thus its kinetic energy also remains constant.
The gravitational potential energy (U) at some height h is equal to the amount of work required to take the object from the ground to that height h.
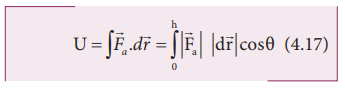
Since the displacement and the applied force are in the same upward direction, the angle between them, θ=0o. Hence, cos00 =1 and |![]() a| = mg and |d
a| = mg and |d![]() | = dr .
| = dr .
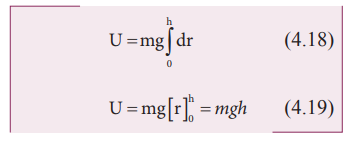
Note that the potential energy stored in the object is defined through work done by the external force which is positive. Physically this implies that the agency which is applying the external force is transferring the energy to the object which is then stored as potential energy. If the object is allowed to fall from a height h then the stored potential energy is converted into kinetic energy.
Solved Example Problems for Potential Energy
Example 4.8
An object of mass 2 kg is taken to a height 5 m from the ground g = 10ms-2 .
a. Calculate the potential energy stored in the object.
b. Where does this potential energy come from?
c. What external force must act to bring the mass to that height?
d. What is the net force that acts on the object while the object is taken to the height ‘h’?
Solution
a. The potential energy U =m g h = 2 × 10 × 5 = 100 J
Here the positive sign implies that the energy is stored on the mass.
b. This potential energy is transferred from external agency which applies the force on the mass.
c.

d. From the definition of potential energy, the object must be moved at constant velocity. So the net force acting on the object is zero.
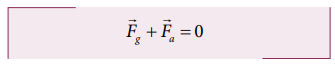
Related Topics