Chapter: 11th Physics : UNIT 4 : Work, Energy and Power
Elastic Potential Energy
Elastic Potential Energy
When a spring is elongated, it develops a restoring force. The potential energy possessed by a spring due to a deforming force which stretches or compresses the spring is termed as elastic potential energy. The work done by the applied force against the restoring force of the spring is stored as the elastic potential energy in the spring.
Consider a spring-mass system. Let us assume a mass, m lying on a smooth horizontal table as shown in Figure 4.9. Here, x = 0 is the equilibrium position. One end of the spring is attached to a rigid wall and the other end to the mass.
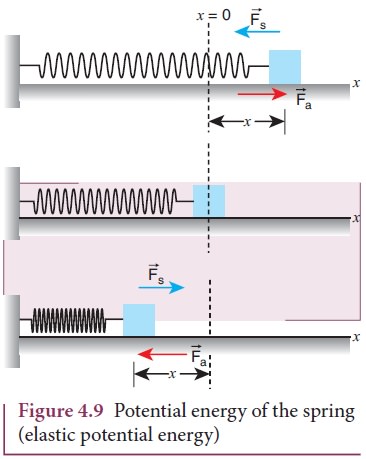
As long as the spring remains in equilibrium position, its potential energy is zero. Now an external force ![]() a is applied so that it is stretched by a distance (x) in the direction of the force.
a is applied so that it is stretched by a distance (x) in the direction of the force.
There is a restoring force called spring force ![]() s developed in the spring which tries to bring the mass back to its original position. This applied force and the spring force are equal in magnitude but opposite in direction i.e.,
s developed in the spring which tries to bring the mass back to its original position. This applied force and the spring force are equal in magnitude but opposite in direction i.e., ![]() a =-
a =-![]() s . According Hooke’s law, the restoring force developed in the spring is
s . According Hooke’s law, the restoring force developed in the spring is

The negative sign in the above expression implies that the spring force is always opposite to that of displacement ![]() and k is the force constant. Therefore applied force is
and k is the force constant. Therefore applied force is ![]() a = + k
a = + k ![]() . The positive sign implies that the applied force is in the direction of displacement
. The positive sign implies that the applied force is in the direction of displacement ![]() . The spring force is an example of variable force as it depends on the displacement
. The spring force is an example of variable force as it depends on the displacement ![]() . Let the spring be stretched to a small distance d
. Let the spring be stretched to a small distance d![]() . The work done by the applied force on the spring to stretch it by a displacement
. The work done by the applied force on the spring to stretch it by a displacement ![]() is stored as elastic potential energy.
is stored as elastic potential energy.

The applied force ![]() a and the displacement d
a and the displacement d![]() (i.e., here dx ) are in the same direction. As, the initial position is taken as the equilibrium position or mean position, x=0 is the lower limit of integration.
(i.e., here dx ) are in the same direction. As, the initial position is taken as the equilibrium position or mean position, x=0 is the lower limit of integration.
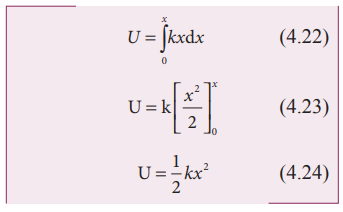
If the initial position is not zero, and if the mass is changed from position xi to xf , then the elastic potential energy is
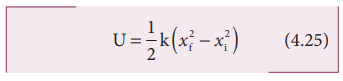
From equations (4.24) and (4.25), we observe that the potential energy of the stretched spring depends on the force constant k and elongation or compression x.
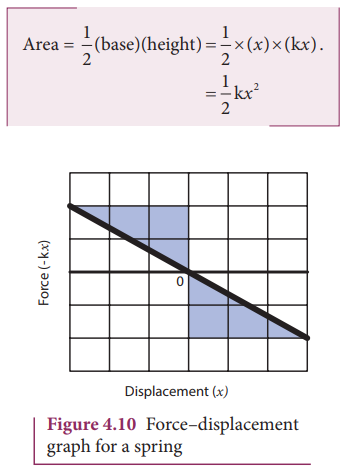
Force-displacement graph for a spring
Since the restoring spring force and displacement are linearly related as F = - k x, and are opposite in direction, the graph between F and x is a straight line with dwelling only in the second and fourth quadrant as shown in Figure 4.10. The elastic potential energy can be easily calculated by drawing a F - x graph. The shaded area (triangle) is the work done by the spring force.
Potential energy-displacement graph for a spring
A compressed or extended spring will transfer its stored potential energy into kinetic energy of the mass attached to the spring. The potential energy-displacement graph is shown in Figure 4.11.

In a frictionless environment, the energy gets transferred from kinetic to potential and potential to kinetic repeatedly such that the total energy of the system remains constant. At the mean position,
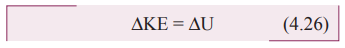
The work done on the springs are stored as potential energy in the springs.

kA>kB implies that UB>UA . Thus, more work is done on B than A.
Solved Example Problems for Elastic Potential Energy
Example 4.9
Let the two springs A and B be such that kA>kB. On which spring will more work has to be done if they are stretched by the same force?
Solution
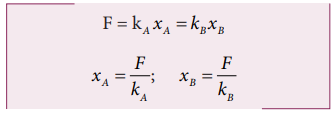
The work done on the springs are stored as potential energy in the springs.

kA>kB implies that UB>UA . Thus, more work is done on B than A.
Example 4.10
A body of mass m is attached to the spring which is elongated to 25 cm by an applied force from its equilibrium position.
a. Calculate the potential energy stored in the spring-mass system?
b. What is the work done by the spring force in this elongation?
c. Suppose the spring is compressed to the same 25 cm, calculate the potential energy stored and also the work done by the spring force during compression. (The spring constant, k = 0.1 N m-1).
Solution
The spring constant, k = 0.1 N m-1
The displacement, x = 25 cm = 0.25 m
a. The potential energy stored in the spring is given by
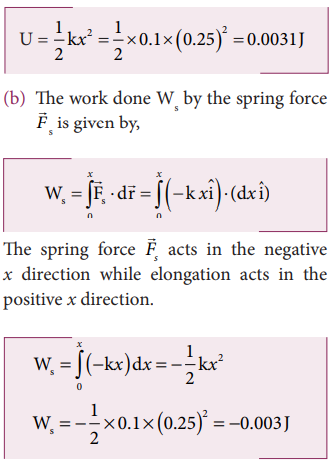
Note that the potential energy is defined through the work done by the external agency. The positive sign in the potential energy implies that the energy is transferred from the agency to the object. But the work done by the restoring force in this case is negative since restoring force is in the opposite direction to the displacement direction.
c. During compression also the potential energy stored in the object is the same.
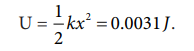
Work done by the restoring spring force during compression is given by
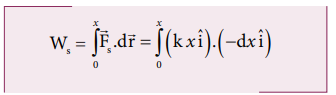
In the case of compression, the restoring spring force acts towards positive x-axis and displacement is along negative x direction.
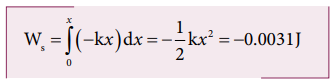
Related Topics