Chapter: 11th Physics : UNIT 4 : Work, Energy and Power
Collisions
COLLISIONS
Collision
is a common phenomenon that happens around us every now and then. For example,
carom, billiards, marbles, etc.,. Collisions can happen between two bodies with
or without physical contacts.
Linear
momentum is conserved in all collision processes. When two bodies collide, the
mutual impulsive forces acting between them during the collision time (∆t)
produces a change in their respective momenta. That is, the first body exerts a
force ![]() 12 on the second body. From Newton’s third
law, the second body exerts a force
12 on the second body. From Newton’s third
law, the second body exerts a force ![]() 21 on the first body.
This causes a change in momentum ∆
21 on the first body.
This causes a change in momentum ∆![]() and ∆
and ∆![]() of the first body and second body
respectively. Now, the relations could be written as,
of the first body and second body
respectively. Now, the relations could be written as,
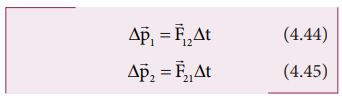
Adding
equation (4.44) and equation (4.45), we get
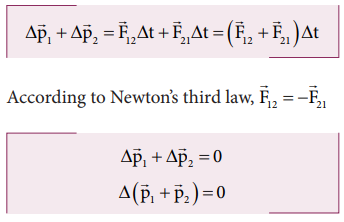
Dividing
both sides by ∆t and taking limit ∆t →0 , we get
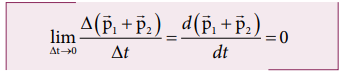
The
above expression implies that the total linear momentum is a conserved
quantity. Note: The momentum is a
vector quantity. Hence, vector
addition has to be followed to find the total momentum of the individual bodies
in collision.
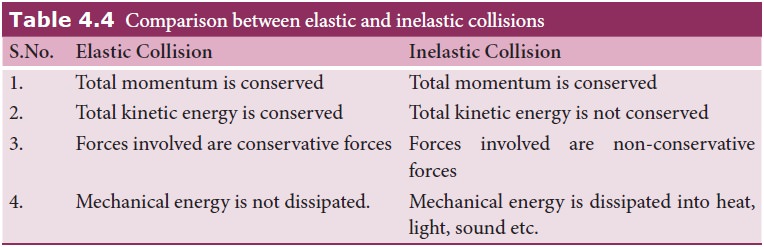
Types of Collisions
In
any collision process, the total linear momentum and total energy are always
conserved whereas the total kinetic energy need not be conserved always. Some
part of the initial kinetic energy is transformed to other forms of energy. This
is because, the impact of collisions and deformation occurring due to
collisions may in general, produce heat, sound, light etc. By taking these
effects into account, we classify the types of collisions as follows:
a.
Elastic collision
b.
Inelastic collision
a. Elastic collision
In
a collision, the total initial kinetic energy of the bodies (before collision)
is equal to the total final kinetic energy of the bodies (after collision)
then, it is called as elastic collision. i.e.,
Total
kinetic energy before collision = Total kinetic energy after collision
b. Inelastic collision
In
a collision, the total initial kinetic energy of the bodies (before collision)
is not equal to the total final kinetic energy of the bodies (after collision)
then, it is called as inelastic collision. i.e.
Total
kinetic energy before collision ≠ Total kinetic energy after collision

Even
though kinetic energy is not conserved but the total energy is conserved. This
is because the total energy contains the kinetic energy term and also a term ∆Q , which includes all the losses that take place during
collision. Note that loss in kinetic energy during collision is transformed to
another form of energy like sound, thermal, etc. Further, if the two colliding
bodies stick together after collision such collisions are known as completely
inelastic collision or perfectly inelastic collision. Such a collision is found
very often. For example when a clay putty is thrown on a moving vehicle, the
clay putty (or Bubblegum) sticks to the moving vehicle and they move together
with the same velocity.
Elastic collisions in one dimension
Consider
two elastic bodies of masses m1
and m2 moving in a straight line (along positive x direction) on a frictionless horizontal surface as shown in
figure 4.16.

In
order to have collision, we assume that the mass m1 moves faster than mass m2 i.e., u1 > u2. For elastic collision, the total
linear momentum and kinetic energies
of the two bodies before and after collision must remain the same.

From
the law of conservation of linear momentum,
Total
momentum before collision ( pi)
= Total momentum after collision ( pf
)
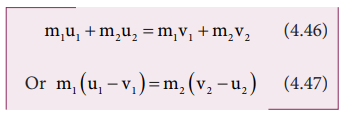
Further,
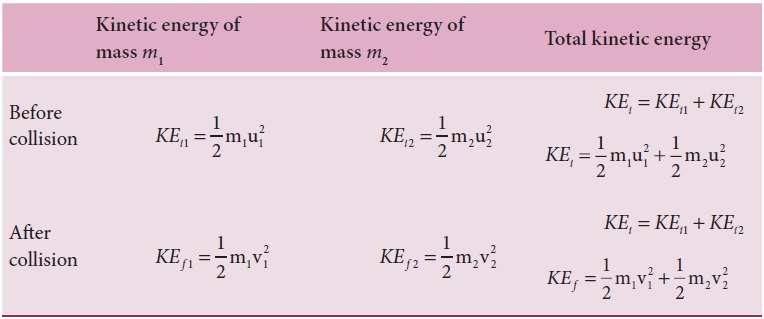
For
elastic collision,
Total
kinetic energy before collision KEi
= Total kinetic energy after collision KE
f
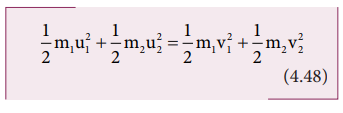
After
simplifying and rearranging the terms,
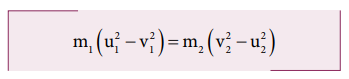
Using
the formula a2 - b2 = (a+b)( a-b) , we can rewrite the
above equation as
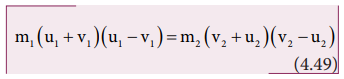
Dividing
equation (4.49) by (4.47) gives,

This
means that for any elastic head on collision, the relative speed of the two
elastic bodies after the collision has the same magnitude as before collision
but in opposite direction. Further note that this result is independent of
mass.
Rewriting
the above equation for v1 and
v2,
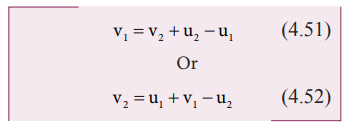
To find the final velocities v1 and v2:
Substituting
equation (4.52) in equation (4.47) gives the velocity of m1 as
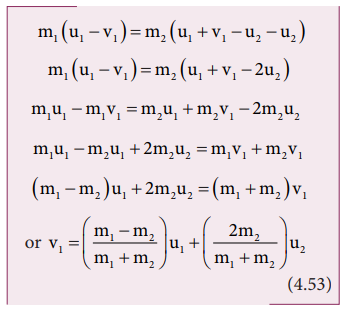
Similarly,
by substituting (4.51) in equation (4.47) or substituting equation (4.53) in
equation (4.52), we get the final velocity of m2 as
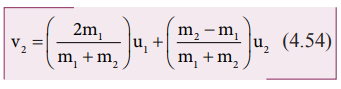
Case 1: When bodies has the same mass i.e., m1 = m2,

The
equations (4.55) and (4.56) show that in one dimensional elastic collision,
when two bodies of equal mass collide after the collision their velocities are
exchanged.
Case 2: When bodies have the same mass i.e., m1 = m2 and second body
(usually called target) is at rest (u2 = 0), By substituting m1 = m2 and u2 = 0 in equations 4.53)
and equations (4.54) we get,
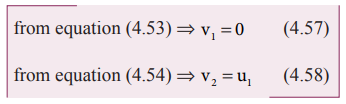
Equations
(4.57) and (4.58) show that when the first body comes to rest the second body
moves with the initial velocity of the first body.
Case 3:
The
first body is very much lighter than the second body 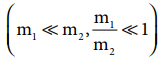
then the ratio m1/m2 ≈ 0 and also if the target is at rest ( u2=0)
Dividing
numerator and denominator of equation (4.53) by m2, we get
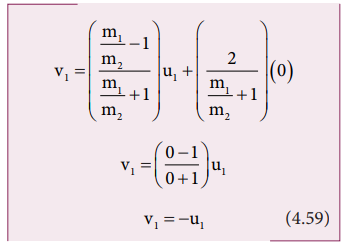
Similarly,
Dividing
numerator and denominator of equation (4.54) by m2, we get

The
equation (4.59) implies that the first body which is lighter returns back
(rebounds) in the opposite direction with the same initial velocity as it has a
negative sign. The equation (4.60) implies that the second body which is
heavier in mass continues to remain at rest even after collision. For example,
if a ball is thrown at a fixed wall, the ball will bounce back from the wall
with the same velocity with which it was thrown but in opposite direction.
Case 4:
The
second body is very much lighter than the first body 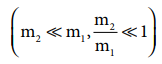
then the ratio m2/m1 ≈ 0 and also if the target is at rest ( u2=0)
Dividing
numerator and denominator of equation (4.53) by m1, we get

Similarly,
Dividing
numerator and denominator of equation (4.58) by m1, we get
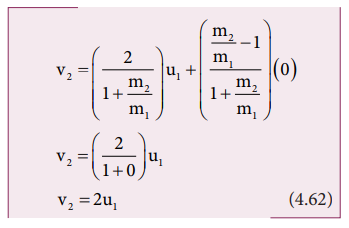
The equation (4.61) implies that the first body which is heavier continues to move with the same initial velocity. The equation (4.62) suggests that the second body which is lighter will move with twice the initial velocity of the first body. It means that the lighter body is thrown away from the point of collision.
Perfect inelastic collision
In
a perfectly inelastic or completely inelastic collision, the objects stick
together permanently aft er collision such that they move with common velocity.
Let the two bodies with masses m1 and m2 move with initial velocities u1
and u2 respectively before collision. Aft er perfect inelastic
collision both the objects move together with a common velocity v as shown in
Figure (4.17).
Since,
the linear momentum is conserved during collisions,
m1u1
+ m2u2 = (m1 + m2)v
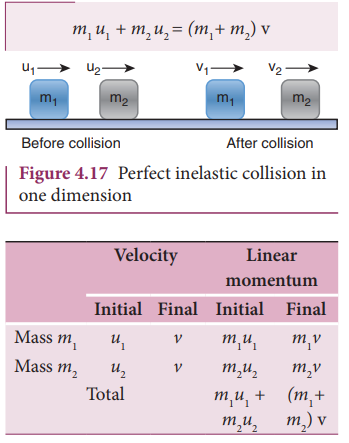
The
common velocity can be computed by
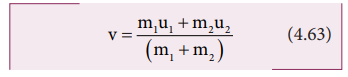
Loss of
kinetic energy in
perfect inelastic collision
In
perfectly inelastic collision, the loss in kinetic energy during collision is
transformed to another form of energy like sound, thermal, heat, light etc. Let
KEi be the total kinetic energy before collision and KEf
be the total kinetic energy after collision.
Total
kinetic energy before collision,
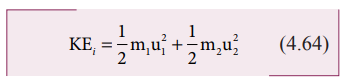
Total
kinetic energy after collision,
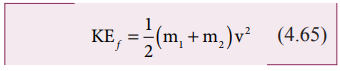
Then
the loss of kinetic energy is Loss of KE,
∆Q = KE i – KEf

Substituting
equation (4.63) in equation (4.66), and on simplifying (expand v by using the
algebra (a+b) 2 = a2+b2+2ab, we get
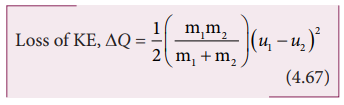
Coefficient
of restitution (e)
Suppose
we drop a rubber ball and a plastic ball on the same floor. The rubber ball
will bounce back higher than the plastic ball. This is because the loss of
kinetic energy for an elastic ball is much lesser than the loss of kinetic
energy for a plastic ball. The amount of kinetic energy after the collision of
two bodies, in general, can be measured through a dimensionless number called
the coefficient of restitution (COR).
It is defined as the ratio of
velocity of separation (relative velocity) after collision to the velocity of
approach (relative velocity) before collision, i.e.,

In
an elastic collision, we have obtained the velocity of separation is equal to
the velocity of approach i.e.,
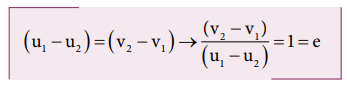
This
implies that, coefficient of restitution for an elastic collision, e =1. Physically, it means that there is no loss of kinetic
energy after the collision. So, the body bounces back with the same kinetic
energy which is usually called as perfect elastic.
In
any real collision problems, there will be some losses in kinetic energy due to
collision, which means e is not always equal to unity. If the ball is perfectly
plastic, it will never bounce back and therefore their separation of velocity
is zero after the collision. Hence, the value of coefficient of restitution, e = 0.
In
general, the coefficient of restitution for a material lies between 0 < e <1.
Solved
Example Problems for collision
Solved Example Problems for Elastic collisions in one dimension
Example 4.20
A lighter particle moving with a speed of 10 m s-1 collides with an object of double its mass moving in the same direction with half its speed. Assume that the collision is a one dimensional elastic collision. What will be the speed of both particles after the collision?
Solution
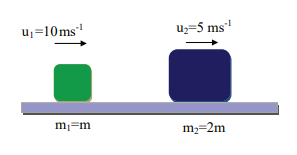
Let the mass of the fi rst body be m which moves with an initial velocity, u1 = 10 m s-1.
Therefore, the mass of second body is 2m and its initial velocity is u2 = ½ u1 = ½(10ms-1)
Then, the fi nal velocities of the bodies can be calculated from the equation (4.53) and equation (4.54)
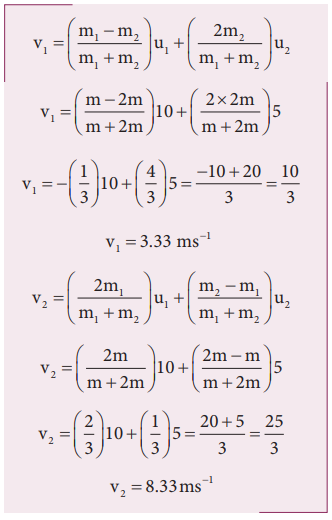
As the two speeds v1and v2 are positive, they move in the same direction with the velocities, 3.33 m s−1 and 8.33 m s−1 respectively.
Solved Example Problems for Perfect inelastic collision
Example 4.21
A bullet of mass 50 g is fired from below into a suspended object of mass 450 g. The object rises through a height of 1.8 m with bullet remaining inside the object. Find the speed of the bullet. Take g = 10 ms-2.
Solution
m1 = 50 g = 0.05 kg; m2 = 450 g = 0.45kg
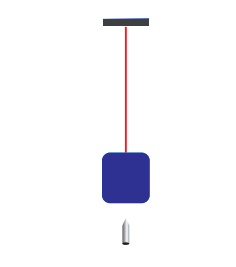
The speed of the bullet is u1. The second body is at rest u2 = 0 . Let the common velocity of the bullet and the object after the bullet is embedded into the object is v.
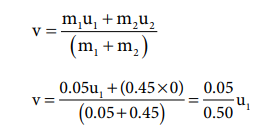
The combined velocity is the initial velocity for the vertical upward motion of the combined bullet and the object. From second equation of motion,
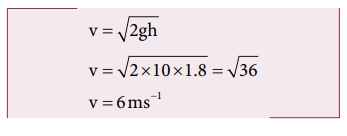
Substituting this in the above equation, the value of u1 is
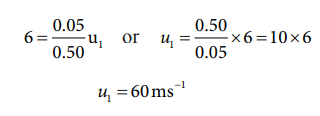
Solved Example Problems for Coefficient of restitution (e)
Example 4.22
Show that the ratio of velocities of equal masses in an inelastic collision when one of the masses is stationary is
v1/v2 = 1-e/1+e
Solution

From the law of conservation of linear momentum,
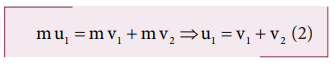
Using the equation (2) for u1 in (1), we get

Related Topics