Long Questions and Answer

Work, Energy and Power | Physics

Long Answer Questions

1. Explain with graphs the difference between work done by a constant force and by a variable force.

Work done by a constance force :

● When a constant force F acts a body the small workdone (dw) by the force in producing a small displacement dr is given by the relation.

dw = (Fcosθ) dr           ………….. (1)

● The total work done in producing a displacement from initial position r_i to final position r_f is

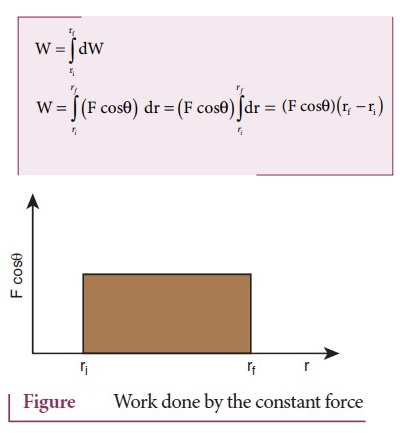
● The graphical representation of the work done by a constant force is shown in figure. The area under the graph shows the work done by the constant force.

Work done by a variable force

● When the component of a variable force F acts on a body, the small work done (dw) by the forces in producing a small displacement dr is given by the relation.

 dw = (F cosθ) dr

Where F and θ are variables

● The total work done for a displacement from initial position r_i to final position r_f is given by the relation,

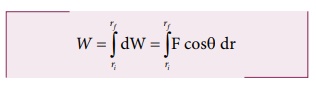
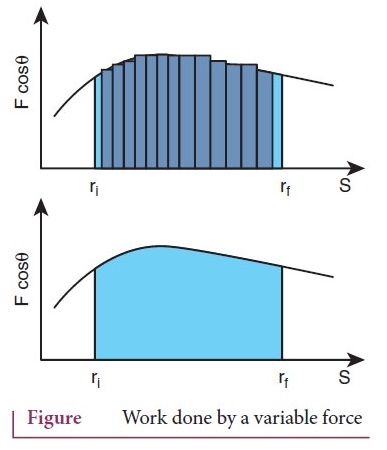
● A graphical representation of the work done by a variable force is shown in figure.

● The area under the graph is the work done by the variable force.

2. State and explain work energy principle. Mention any three examples for it.

Statement :-

● It states that the work done by the force on the body changes the kinetic energy of the body. This called work - kinetic energy theorem.

● Work and energy are equivalents. This is true in the case of kinetic energy also.

● To prove this, let us consider a body of mass at rest on friction less horizontal surface.

● The work done (w) by the constant force (F) for a displacement (s) in the same direction is.

W = F_s              ……………. (1)

● The constant force is given by the equation

F = ma                ……………… (2)

● The third equation of motion can be written as

v² = u² + 2as

a = [ v² - u² ] / 2s

● Substituting for 'a' in equation (2)

F = m ( [v² − u² ] / 2s)

● Substituting equation (3) in (1)

W = m ([v² / 2s] s) – m ([u² / 2s] s)

W = 1/2 mv² – 1/2 mu²       ………… (4)

The expression for kinetic energy

● The term (1/2 mv²) in the above equation is the kinetic energy of the body of mass (m) moving with velocity (v)

K.E = 1/2 mv²        ………….. (5)

● Kinetic energy of the body is always positive.

● From equation (4) and (5)

KE = 1/2 mv² − 1/2 mv²       ……………….(6)

Thus W = ∆KE

The expression on the right hand side (RHS) of equation (6) is change in kinetic energy of the body. The work - kinetic energy implies the following

1. If the work done by the force on the body is positive, then its kinetic energy increases.

2. If the work done by the force on the body is negative, then kinetic energy decreases.

3. If there is no work done by the force on the body then there is no change in its kinetic energy, which means that the body has moved at constant speed provided its mass remains constant.

3. Arrive at an expression for power and velocity. Give some examples for the same.

● The work done by a force  for a displacement d is

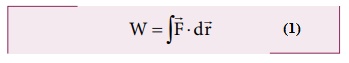         …………(1)

● Left hand side of the equation (1) can be written as

W = ʃ dw = ʃ dw/dt dt            …………….. (2)

 (Multiplied and divided by dt)

● Since, velocity is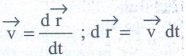 

● Right hand side of the equation (1) can be written as

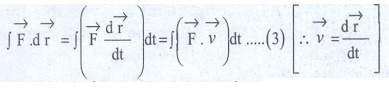
● Substituting equation (2) and (3) in equaiton (1) we get,

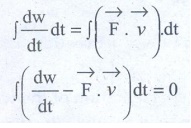
………..(3) 

● The relation is true for any arbitrary value of dt. This implies that the term with in the bracket must be equal to zero,

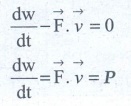
4. Arrive at an expression for elastic collision in 1 Dimension and discuss various cases.

● Consider two elastic bodies of masses m₁ and m₂ moving in a straight line (along positive x direction) on a friction less horizontal surface as shown in figure.

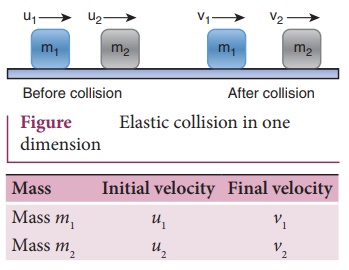
● The mass m₁ moves faster than mass m₂ (i.e. u₁ > u₂). For elastic collision, the total linear momentum and kinetic energies of the two bodies before and after collision must remain the same.

● From the law of conservation of linear momentum

Total momentum before collision (p_i) = Total momentum after collision (p_f)

● m₁u₁+ m₂u₂ = m₁v₁+ m₂v₂ …………. (1)

m₁(u₁ - v₁) = m₂ (v₂ - u₂) ……….. (2)

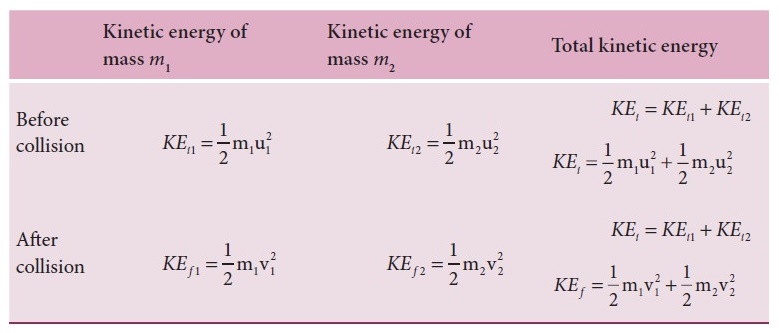
● For elastic collision

Total kinetic energy before collision KE_i = Total kinetic energy after collision KE_f

1/2 m₁u₁² + 1/2 m₂u₁² = 1/2 m₁v₁² + 1/2 m₁v₂²      ………(3)

m₁(u₁² − v₁²) = m₂ (v₂² − u₂² )

● Using formula a² − b² = (a+b) (a-b) we can rewrite above equation as,

m₁ (u₁+v₁) (u₁−v₁) = m₂ (v₂+u₂) (v₂−u₂)          ………….. (4)

Dividing (4) by (2) gives,

[ m₁ (u₁+v₁)(u₁−v₁) ] / [ m₁ (u₁−v₁) ] = [ m₂ (v₂+u₂)(v₂-u₂) ] / [ m₂(v₂-u₂) ]

u_l + v_l = v₂ - u₂         ………… (5)

Rearranging (5) we get,

u₁+u₂ = v₂ - v₁

Equation (5) can be re written as,

u₁−u₂ = − (v₁−v₂)

● For any elastic head on collision, the relative speed of the two elastic bodies after the collision has the same magnitude as before collision but in opposite direction.

Rewritting the above equation for and v₁ and v₂

v₁ = v₂ + u₂ − u₁    …………..(6)

(or) v₂ = u₁ + v₁ − u₂       ……... (7)

To find the velocities of v₁ and v₂

Substituting equation (7) in equation (2) gives the velocity of mass m₁ as

m₁ (u₁- v₁) = m₂ (u₁ + v₁ - u₂ - u₂)

m₁ (u₁- v₁) = m₂ (u₁ + v₁ - 2u₂ )

m₁ u₁- m₁v₁ = m₂u₁ + m₂v₁ - 2m₂ u₂

m₁ u₁ - m₂ u₁ + 2m₂u₂ = m₁v₁ + m₂v₁

(m₁ - m₂ )u₁ + 2m₂u₂ = (m₁ + m₂) v₁

v₁ = (m₁-m₂ / m₁+m₂) u₁ + (2m₂ / m₁+m₂) u₂     ………(8)

● Similarly by substituting (6) in equation (2) (or) substituting equation (8) in equation (7) we get the final velocity of m₂ as,

v₂ = (2m₁ / m₁+m₂ ) u₁ + (m₂ - m₁ / m₁ + m₂) u₂       ………(9)

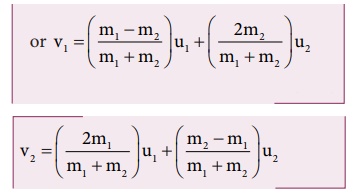
Case : I When bodies has the same mass

(i.e.) m₁ = m₂

Equation (8) ⇒ v₁ = (0) u₁ + (2m₂ / 2m₂) u₂

v₁ = u₂      ………………(10)

Equation 9 ⇒ v₂ = (2m₁ / 2m₁) u₁ + (0)u₂   

V₂ = u₁    ……… (11)

The equation (10) and (11) show that in one dimensional elastic collision, when two bodies of equal mass collide after the collision their velocities are exchanged.

Case 2: When bodies have the same mass (Q) m₁ = m₂ and second body (usually called target) is at rest (u₂ = 0)

By substituting m₁ = m₂ and u₂ = 0 in equations (8) and (9) we get,

from equation (8) ⇒ v₁ = 0  ……….. (12)

from equation (9) ⇒ v₂= u₁     ……….. (13)

Equation (12) and (13) shows that when the first body comes to rest the second body moves with initial velocity of the first body.

Case 3: The first body is very much lighter than the second body.

(m₁ << m₂ ; m₁ / m₂ << 1) then the ratio m₁ / m₂ = 0 and also if the target is at rest (u₂ = 0). Dividing numerator and denominator of equations (8) by m₂ we get,

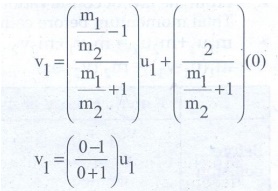
v₁ = − u₁         ……………..(14)

● Similiarly dividing numerator and denominator of equation (9) by m₂ we get,

v₂ = 0          ………..(15)

● The equation (14) implies that the first body which is lighter returns back (rebounds) in the opposite direction with the same initial velocity as it has a negative sign. The equation (15) implies that the second body which is heavier mass continues to remain at rest even after collision. For example if a ball is thrown at a fixed wall, the ball will bounce back from the wall with the same velocity with which it was thrown but in opposite direction.

Case 4: The second body is very much lighter then the first body (m₂ << m₁, m₂/m₁<<1) then the ratio m₂/m₁ = 0 and also if the target is at rest (u₂ = 0).

● Dividing numerator and denominator of equation (8) by m₁ we get,

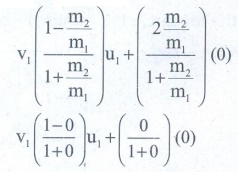
v₁ = u₁   ……………(16)

● Similarly dividing numerator and denominator of equation (13) by m₁ we get,

v₂ = u₂      ……………(17)

● The equation (16) implies that the first body which is heavier continues to move with the same initial velocity.

● The equation (17) suggests that the second body which is lighter will move twice the initial velocity of the first body. It means that the lighter body is thrown away from the point collision.

5. What is inelastic collision? In which way it is different from elastic collision. Mention few examples in day to day life for inelastic collision.

● In a collision the total initial kinetic energy of the bodies (before collision) is not equal to the total final kinetic energy of the bodies (after collision) then, it is called as in elastic collision.

i.e. Total kinetic energy before collision ≠ Total kinetic energy after collision

● Total kinetic energy after collision − Total kinetic energy before collision = Loss in energy during collision = ∆Q

● Even though kinetic energy is not conserved but the total energy is conserved.

● This is because the total energy contains the kinetic energy term and also a term ∆Q, which includes all the losses that take place during collision.

● Note that loss in kinetic energy during collision is transformed to another form of energy like, sound thermal etc.

● Further, if the two colliding bodies stick together after collision such collisions are known as completely in elastic collision (or) perfectly in elastic collision.

● For example when a clay putty is thrown on a moving vehicle, the clay putty (or bubble gum) sticks to the moving vehicle and they move together with the same velocity.