Chapter: 11th Physics : UNIT 4 : Work, Energy and Power

Conservative and non-conservative forces

A force is said to be a conservative force if the work done by or against the force in moving the body depends only on the initial and final positions of the body and not on the nature of the path followed between the initial and final positions.

Conservative and non- conservative forces

Conservative force

Let us consider an object at point A on the Earth. It can be taken to another point B at a height h above the surface of the Earth by three paths as shown in Figure 4.12.

Whatever may be the path, the work done against the gravitational force is the same as long as the initial and final positions are the same. This is the reason why gravitational force is a conservative force. Conservative force is equal to the negative gradient of the potential energy. In one dimensional case,

Examples for conservative forces are elastic spring force, electrostatic force, magnetic force, gravitational force, etc.

Non-conservative force

A force is said to be non-conservative if the work done by or against the force in moving a body depends upon the path between the initial and final positions. This means that the value of work done is different in different paths.

1. Frictional forces are non-conservative forces as the work done against friction depends on the length of the path moved by the body.

2. The force due to air resistance, viscous force are also non-conservative forces as the work done by or against these forces depends upon the velocity of motion.

The properties of conservative and non-conservative forces are summarized in the Table 4.3.

Solved Example Problems for Conservative and nonconservative forces

Example 4.11

Compute the work done by the gravitational force for the following cases

Solution

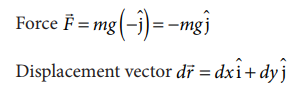
(As the displacement is in two dimension; unit vectors and are used)

a. Since the motion is only vertical, horizontal displacement component dx is zero. Hence, work done by the force along path 1 (of distance h).

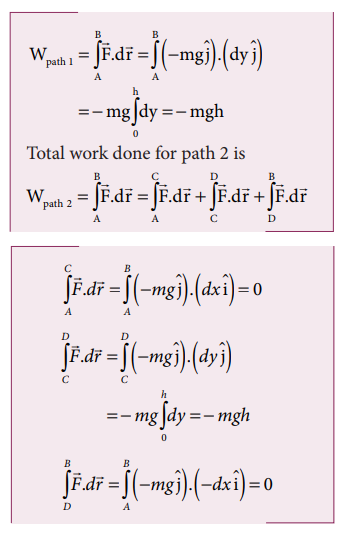
Therefore, the total work done by the force along the path 2 is

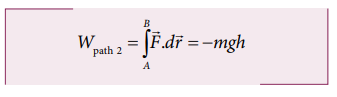
Note that the work done by the conservative force is independent of the path.

Example 4.12

Consider an object of mass 2 kg moved by an external force 20 N in a surface having coefficient of kinetic friction 0.9 to a distance 10 m. What is the work done by the external force and kinetic friction ? Comment on the result. (Assume g = 10 ms-2)

Solution

m = 2 kg, d = 10 m, Fext = 20 N, k = 0.9. When an object is in motion on the horizontal surface, it experiences two forces.

a. External force, Fext = 20 N

b. Kinetic friction,

fk =μkmg = 0.9x(2)x10=18N.

The work done by the external force Wext = Fs = 20x20 =200J

The work done by the force of kinetic friction Wk =fkd = (-18) x10=-180J Here the negative sign implies that the force of kinetic friction is pposite to the direction of displacement.

The total work done on the object

Wtotal = Wext + Wk = 200 J – 180 J = 20 J .

Since the friction is a non-conservative force, out of 200 J given by the external force, the 180 J is lost and it can not be recovered.

Study Material, Lecturing Notes, Assignment, Reference, Wiki description explanation, brief detail

11th Physics : UNIT 4 : Work, Energy and Power : Conservative and non-conservative forces |