Work, Energy and Power | Physics - Short Questions and Answer | 11th Physics : UNIT 4 : Work, Energy and Power
Chapter: 11th Physics : UNIT 4 : Work, Energy and Power
Short Questions and Answer
Work, Energy and Power (Physics)
Short Answer Questions
1. Explain how the definition of work in physics is different from general percep-tion.
●
Work refers to both physical as well as mental work. In fact, any activity can
generally be called as work.
●
But in physics, the term work is treated as physical quantity with precise
definition.
●
Work is said to be done by the force when the force applied on the body
displaces it.
2. Write the various types of potential energy. Explain the formulae.
i)
The energy possesed by the body due to gravitational force gives rise to
gravitational potential energy
u
= mgh
Where,
m is mass of the body
g
is acceleration due to gravity
h
is the height of the body above the ground.
ii)
The energy due to spring force and other similar forces gives rise to elastic
potential energy.
U
= 1/2 k(xf2 – xi2)
Where,
k is the force constant
xi
is the initial position of the spring
xf
is the final position of the spring
iii)
The energy due to electro static force on charge gives rise to electrostatic
potential energy.
U
= q1q2 / 4πεor
Where,
q1, q2 are the point charges
r
is the distance between two point charges
εo
is the permitivity of free space
εo
= 8.854 × 10-12 C2N-1m-2
3. Write the differences between conservative and Non-conservative forces. Give two examples each.

Conservaive
forces
1.
Work done is independent of the path
2.
Work done in a round trip is zero
3.
Total energy remains constant
4.
Work done is completely recoverable
5.
Force is the negative gradient of potential
6.
Examples:
i.
Elastic spring force
ii.
Electrostatic force
iii.
Magnetic force
iv.
Gravitational force
Non
- Conservaive forces
1.
Work done depends upon the path
2.
Work done in a round trip is not zero
3.
Energy is dissipated as heat energy
4.
Work done is not completely recoverable
5.
No such relation exists.
6.
Examples:
i.
Force due to air resistance
ii.
Viscous force.
4. Explain the characteristics of elastic and inelastic collision.
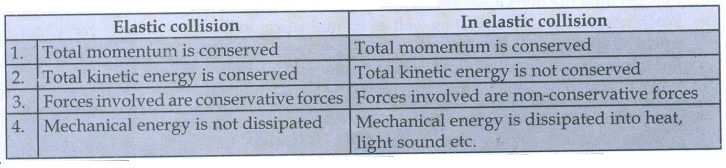
Elastic
collision
1.
Total momentum is conserved
2.
Total kinetic energy is conserved
3.
Forces involved are conservative forces
4.
Mechanical energy is not dissipated
In
elastic collision
1.
Total momentum is conserved
2.
Total kinetic energy is not conserved
3.
Forces involved are non-conservative forces
4.
Mechanical energy is dissipated into heat, light sound etc.
5. Define the following
a) Coefficient of restitution
b) Power
c) Law of conservation of energy
d) loss of kinetic energy in inelastic collision.
a)
Co-efficient of restitution
It
is defined as the ratio of velocity of separation (relative veloctiy) after
collision to the velocity of approach (relative velocity) before collision.
e = Velocity of separation (after collision) /
Velocity of approach (before collision);
e = (v2−v1) / (u1−u2)
b)
Power
It
is defined as the rate of wrok done (or) energy delivered.
Power
(P) = Work done (w) / time taken (t)
P
= w / t
c)
Law of conservation of energy
It
states that energy can neither be created nor be destroyed. It may be transformed
from one form to another but total energy of an isolated system remains
constant.
d)
Loss of kinetic energy in inelastic collision
●
In perfect inelastic collision, the loss in kinetic energy during collision is
transformed to another form of energy like sound, thermal, heat, light etc.
●
Let KEi be the total kinetic enrergy before collision and KEf
be the total kinetic energy after collision.
●
Total kinetic energy before collision
KE1
= 1/2 m1u12 + 1/2 m2u22
………….(1)
●
Total kinetic energy after collision
KEf
= 1/2 (m1+m2)v2 …………………(2)
●
Then the loss of kinetic energy, ∆Q = KEi − KEf
∆Q
= 1/2 m1u12 + 1/2 m2u22
− 1/2 (m1+m2)v2 ………….(3)
●
Substituting equation v = [ m1u1 + m2u2
] / (m1+m2) in equafion (3) and On simpiytying, we get loss of K.E ∆Q =
1/2 (m1m2 / [m1+m2] ) (u1–u2)2
Related Topics