Chapter: 11th Physics : UNIT 4 : Work, Energy and Power
Motion in a vertical circle
Motion in a vertical circle
Imagine that a body of mass (m) attached to one end of a massless and inextensible string executes circular motion in a vertical plane with the other end of the string fixed. The length of the string becomes the radius ( ![]() ) of the circular path (Figure 4.14).
) of the circular path (Figure 4.14).
Let us discuss the motion of the body by taking the free body diagram (FBD) at position where the position vector ( ![]() ) makes an angle θ with the vertically downward direction and the instantaneous velocity is as shown in Figure 4.14.
) makes an angle θ with the vertically downward direction and the instantaneous velocity is as shown in Figure 4.14.
There are two forces acting on the mass.
1. Gravitational force which acts downward
2. Tension along the string.
Applying Newton’s second law on the mass, In the tangential direction,
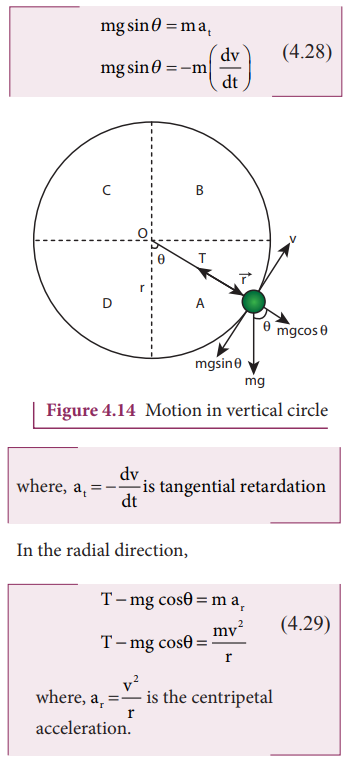
The circle can be divided into four sections A, B, C, D for better understanding of the motion. The four important facts to be understood from the two equations are as follows:
i. The mass is having tangential acceleration (g sin θ) for all values of θ (except θ = 0o), it is clear that this vertical cirular motion is not a uniform circular motion.
ii. From the equations (4.28) and (4.29) it is understood that as the magnitude of velocity is not a constant in the course of motion, the tension in the string is also not constant.
iii. The equation T = mg cosθ + mv2/r highlights that in sections A and D of the circle, (for –π/2 < θ < π/2;cosθ is positive) , the term mg cosθ is always greater than zero. Hence the tension cannot vanish even when the velocity vanishes.
iv. The equation mv2/r = T - mg cosθ further highlights that in sections B and D of the circle, (for –π/2 < θ < 3π/2;cosθ is negative) the second term is always greater than zero. Hence velocity cannot vanish, even when the tension vanishes.
These points are to be kept in mind while solving problems related to motion in vertical circle.

For the lowest point (1)
When the body is at the lowest point 1, the gravitational force m ![]() which acts on the body (vertically downwards) and another one is the tension
which acts on the body (vertically downwards) and another one is the tension ![]() 1 acting vertically upwards, i.e. towards the center. From the equation (4.29), we get
1 acting vertically upwards, i.e. towards the center. From the equation (4.29), we get

For the highest point (2)
At the highest point 2, both the gravitational force m![]() on the body and the tension
on the body and the tension ![]() 2 act downwards, i.e. towards the center again.
2 act downwards, i.e. towards the center again.
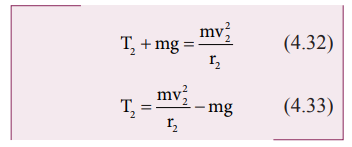
From equations (4.31) and (4.33), it is understood that T1 > T2. The difference in tension T1 - T2 is obtained by subtracting equation (4.33) from equation (4.31).
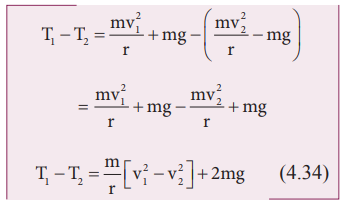
The term [v12 – v22] can be found easily by applying law of conservation of energy at point 1 and also at point 2.

From the law of conservation of energy given in equation (4.35), we get

Minimum speed at the highest point (2)
The body must have a minimum speed at point 2 otherwise, the string will slack before reaching point 2 and the body will not loop the circle. To find this minimum speed let us take the tension T2 = 0 in equation (4.33).
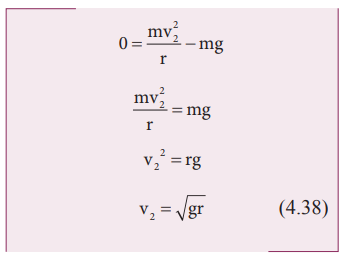
The body must have a speed at point 2, v2 ≥ √gr to stay in the circular path.
Minimum speed at the lowest point 1
To have this minimum speed (v2=√gr) at point 2, the body must have minimum speed also at point 1.
By making use of equation (4.36) we can find the minimum speed at point 1.

The body must have a speed at point 1, v1≥√5gr to stay in the circular path.
From equations (4.38) and (4.39), it is clear that the minimum speed at the lowest point 1 should be √5 times more than the minimum speed at the highest point 2, so that the body loops without leaving the circle.
Solved Example Problems for Motion in a vertical circle
Example 4.17
Water in a bucket tied with rope is whirled around in a vertical circle of radius 0.5 m. Calculate the minimum velocity at the lowest point so that the water does not spill from it in the course of motion. (g = 10 ms-2)
Solution

Related Topics