Vibrations of air column in Organ pipes

Vibrations of air column in pipes

Musical wind instruments like flute, clarinet etc. are based on the principle of vibrations of air columns. Due to the superposition of the incident wave and the reflected wave, longitudinal stationary waves are formed in the pipe.

1.Organ pipes

Organ pipes are musical instruments which are used to produce musical sound by blowing air into the pipe. Organ pipes are two types

 (i) closed organ pipes, closed at one end

(ii) open organ pipe, open at both ends.

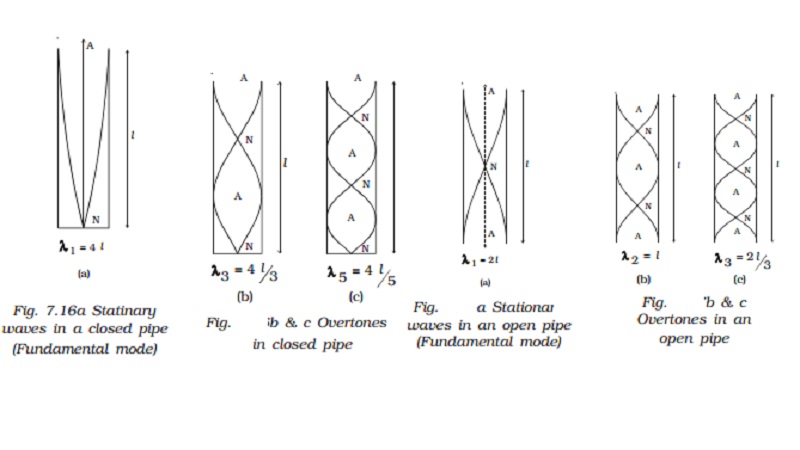
Closed organ pipe : If the air is blown lightly at the open end of the closed organ pipe, then the air column vibrates (Fig. a) in the fundamental mode. There is a node at the closed end and an antinode at the open end. If l is the length of the tube.

l = λ₁/4

or

λ₁ = 4l

If n₁ is the fundamental frequency of the vibrations and v is the velocity of sound in air, then

n1 = v / λ₁ = v/4l

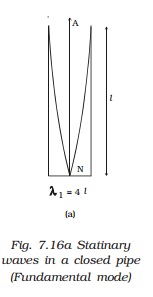
If air is blown strongly at the open end, frequencies higher than fundamental frequency can be produced. They are called overtones. Fig. b & Fig. c shows the mode of vibration with two or more nodes and antinodes.

l=3 λ₃/4 or λ₃=4l/3

n₃ = v/ λ₃=3v/4l=3n₁

This is the first overtone or third harmonic.

Similarly n₅ =5v/4l=5n₁

This is called as second overtone or fifth harmonic.

Therefore the frequency of pth overtone is (2p + 1) n₁ where n1 is the fundamental frequency. In a closed pipe only odd harmonics are produced. The frequencies of harmonics are in the ratio of 1 : 3 : 5.....

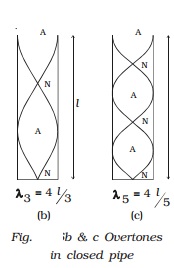
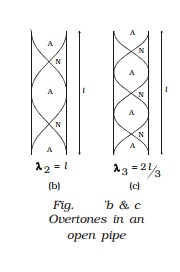
(ii) Open organ pipe - When air is blown into the open organ pipe, the air column vibrates in the fundamental mode Fig. a. Antinodes are formed at the ends and a node is formed in the middle of the pipe. If l is the length of the pipe, then

l= λ₁/2 

or

λ₁=2l

v=n₁ λ₁₌ n₁ 2 l

The fundamental frequency

n₁=v/2 l

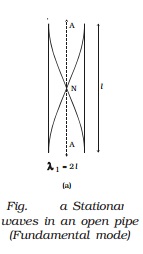
In the next mode of vibration additional nodes and antinodes are formed as shown in Fig. b and Fig. c.

l = λ₂ or v = n₂λ₂ = n₂ . l

∴ n₂ =(v/l)=2n₁

This is the first overtone or second harmonic.

Similarly, n₃ =v/ λ₃=3v/2l=3n₁

This is the second overtone or third

harmonic.

Therefore the frequency of P^th overtone is (P + 1) n₁ where n1 is the fundamental frequency.

The frequencies of harmonics are in the ratio of 1 : 2 : 3 ....