Chapter: 11th 12th std standard Class Physics sciense Higher secondary school College Notes
Velocity of wave in different media
Velocity of wave in different media
The
velocity of mechanical wave depends on elasticity and inertia of the medium.
Velocity of a
transverse wave along a stretched string
Let
us consider a string fixed at one of its ends and tension be applied at the
other end. When the string is plucked at a point, it begins to vibrate.
Consider a transverse
wave proceeding from left to right in the form of a pulse when
the string is plucked at a point as shown in Fig.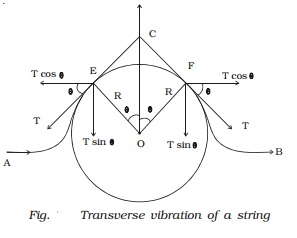 
. EF is the displaced
position of the string at an instant of time. It forms an arc of a circle with
O as centre and R as radius. The arc EF subtends an angle 2θ at O.
If
m is the mass per unit length of the string and dx is the length of the arc EF,
then the mass of the portion of the string is m dx.
∴ Centripetal force
= (
m.dx.v2 ) / R
This
force is along CO. To find the resultant of the tension T at the points E and
F, we resolve T into two components Tcos θ and T sinθ.
T
cosθ components acting
perpendi- cular to CO are of equal in magnitude but opposite in direction, they
cancel each other.
T
sin θ components act parallel to CO. Therefore the
resultant of the tensions acting at E and F is 2T sin θ. It is directed along CO. If θ is small, sinθ =
θ and the resultant
force due to tension is 2Tθ.
resultant force = 2Tθ
= 2T dx/2R
=
T.dx/R ???.(2)
For
the arc EF to be in equilibrium,
m.dx
v2 / R = T.dx / R
v2
= T/m
v=root(T/m) ???.(3)
Velocity of longitudinal waves in
an elastic medium
Velocity
of longitudinal waves in an elastic medium is
V=
root(E/ρ ) ????(1)
where
E is the modulus of elasticity, ρ is the density of the medium.
(i)
In the case of a solid rod
v=
root(q/p) ????..(2)
where
q is the Young?s modulus of the material of the rod and ρ is the density of the
rod.
(ii)
In liquids, v = root(x/p) ??(3)
where
k is the Bulk modulus and ρ is the density of the liquid.
Newton?s formula for
the velocity of sound waves in air
Newton assumed that
sound waves travel through air under isothermal conditions (i.e) temperature of
the medium remains constant.
The change in pressure
and volume obeys Boyle?s law.
PV = constant
Differentiating, P . dV
+ V .dP = 0
P. dV = ?V dP
P
= -dP/(dV/V) = change in pressure / volume strain
P
= k (Volume Elasticity
Therefore
under isothermal condition, P = k
v=
root(k/p) = root(P/p)
where P is the pressure of air and is the density of air. The above equation is
known as Newton?s formula for the velocity of sound waves in a gas.
At NTP, P = 76 cm of mercury
= (0.76 ? 13.6 ? 103
? 9.8) N m?2 = 1.293 kg m?3.
Velocity of sound in
air at NTP is
v = 280 m s?1
The experimental value
for the velocity of sound in air is 332 m s?1. But the theoretical
value of 280 m s?1 is 15% less than the experimental value. This
discrepancy could not be explained by Newton?s formula.
Related Topics