Questions with Answers, Solution | Numbers | Chapter 1 | 8th Maths - Try these, Recap Exercise, Student Activities, Think and answer | 8th Maths : Chapter 1 : Numbers
Chapter: 8th Maths : Chapter 1 : Numbers
Try these, Recap Exercise, Student Activities, Think and answer
Recap Exercise
1.The simplest form of 125/200 is _________.
Solution: 125/200 = [125 ÷ 25] / [200 ÷ 25] = 5/8
[Answer: 5/8]
2. Which of the following is not an equivalent fraction of 8/12 ?
(A) 2/3
(B) 16/24
(C) 32/60
(D) 24/36
[Answer: (C) 32/60]
Solution:
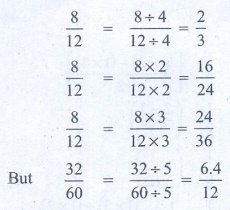
∴ 32 / 60 is not an equivalent fraction of 8 / 12.
3.Which is bigger: 4/5 or 8/9 ?
Solution:
LCM of 5 and 9 = 45
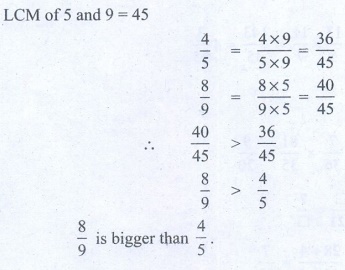
4.Add the fractions:3/5 + 5/8 + 7/10
Solution:

LCM of 5, 8, 10 = 5 × 2 × 4
= 40
3/5 + 5/8 + 7/10 = [ (3 × 8) + (5 × 5) + (7 × 4) ] / 40
= [24 + 25 + 28] / 40
= 77 / 40 = 1 (37/40)
5.Simplify: 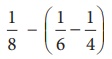
Solution:
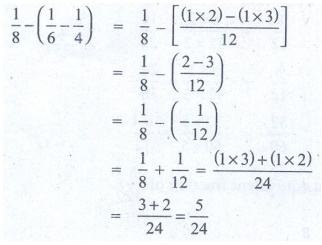
1/8 – (1/6 – 1/4) = 1/8 – { [(1 × 2) − (1 × 3) ] / 12 }
= 1/8 – ( [2−3] / 12 )
= 1/8 – ( − 1/12 )
= 1/8 + 1/12 = [(1 × 3) + (1 × 2)] / 24
= [3 + 2] / 24 = 5 / 24
6. Multiply: 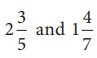
Solution:
2 (3/5) × 1 (4/7) = (13/5) × (11/7) = 143/35 = 4 (3/35)
7.Divide: 7/36 by 35/81
Solution:
7/36 ÷ 35/81 = 7/36 × 81/35 = 9/20
8. Fill in the boxes: 
Solution:
28/44 = [28 ÷ 4] / [44 ÷ 4] = 7 / 11
7/11 = 28 / 44 = 42 / 66 = 70 / 110 = 77 / 121
42 / 66 = 70 / 110 = 28 / 44 = 77 / 121 = 7 / 11 .
9. In a city 7/20 of the population are women and 1/4 are children. Find the fraction of the fraction of the population of men.
Solution:
Let the total population = 1
Population of men = Total population − Women − Children
= 1 – 7/20 – 1/4 = 20/20 – 7/20 – 5/20
= [20 – 7 – 5] / 20 = 8/20 = 2/5
∴ Population of men = 2/5
10. Represent (1/2 – 1/4) by a diagram.
Solution:
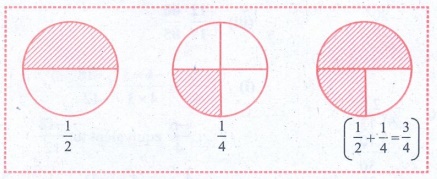
Try these
1. Is the number –7 a rational number? Why?
Solution:
Yes
– 7 is a rational number. Because – 7 = −14 / 2 = p / q
2. Write any 6 rational numbers between 0 and 1.
Solution:
1/2, 1/3, 1/4, 1/5, 1/6, 1/7
Activity
Use a string as a number line and fix it on the wall, for the length of the class room. Just mark the integers spaciously and ask the students to pick the rational number cards from a box and fix it roughly at the right place on the number line string. This can be played between teams and the team which fixes more number of cards correctly (by marking) will be the winner.

Try these
Write the decimal forms of the following rational numbers:
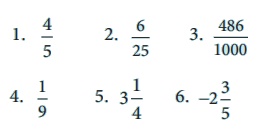
Solution:

1. 4/5 = [4 × 20] / [5 × 20] = 80 / 100 = 0.80
2. 6/25 = [6 × 4] / [25 × 4] = 24 / 10 = 0.24
3. 486/1000 = 0.486
Try These
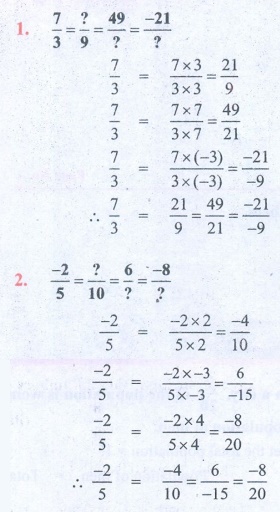
1. 7/3 = ?/9 = 49/? = −21/?
7/3 = [7 × 3] / [3 × 3] = 21 / 9
7/3 = [7 × 7] = [3 × 7] = 49 / 21
7 / 3 = [7 × (−3)] / [3 × (−3)] = −21 / −9
∴ 7/3 = 21/9 = 49/21 = −21/−9
2. −2 / 5 = ? / 10 = 6 / ? = −8 / ?
−2 / 5 = [−2 × 2] / [5 × 2] = −4 / 10
−2 / 5 = [−2 × −3] / [ 5 × −3] = 6 / −15
−2 / 5 = [−2 × 4] / [5 × 4] = −8 / 20
∴ −2 / 5 = [−4 / 10] = 6 / −15 = −8 / 20
Try these
1. Which of the following pairs represents equivalent rational numbers?
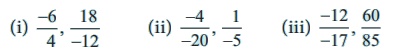
(i) −6/4, 18/−12
−6/4 = [−6 × 3] / [4 × 3] = −18 / 12
∴ −6 / 4 = equivalent to −18 / 12
(ii) −4/−20, 1/−5
−4/−20 = [−4 ÷ (−4)] / [−20 ÷ (−4)] = 1/5 ≠ −1/5
∴ −4 / −20 not equivalent to 1 / −5
(iii) −12/−17, 60/85
−12 / −17 = [−12 × −5] / [−17 × −5] = 60 / 85
∴ −12 / −17 equivalent to 60 / 85
2. Find the standard form of:
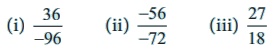
(i) 36/−96 = [−36 ÷ 12] / [96 ÷ 12] = −3 / 8
(ii) −56/−72 = [−56 ÷ (−8)] / [−72 ÷ (−8)] = 7 / 9
(iii) 27/18 = 1 (9/18) = 1 (1/2)
3. Mark the following rational numbers on a number line.
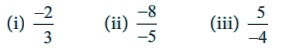
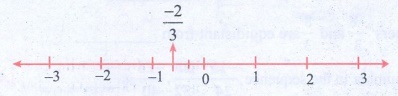
Solution:
(i) −2 / 3
−2/3 lies between 0 and −1.
The unit part between 0 and −1 is divided into 3 equal parts and second part taken.
(ii) −8 / −5
−8/−5 = 1 (3/5)
1 (3/5) lies between 1 and 2. The unit part between 1 and 2 is divided into 5 equal parts and the third part is taken.

(iii) 5 / −4
5 / −4 = − 5/4 = − 1 ¼
−1 (1/4) lies between −1 and −2. The unit part between −1 and −2 is divided into four equal parts and the first part is taken.

Think
Are there any rational numbers between −7/11 and 6/−11 ?
Solution:
−7/11 = −70/110 ; 6/−11 = −60/110
−61/110, −62/110 …. −69/110
∴ Thre are many rational numbers between −7/11 and 6/−11
Think
Is zero a rational number? If so, what is its additive inverse?
Solution: Yes zero is a national number. Additive inverse of zero is zero.
Think
What is the multiplicative inverse of 1 and –1?
Solution: Multiplicative inverse of 1 is 1 and −1 is −1.

Solution:
(i) −7/3 ÷ 5 = [−7/3] ÷ [5/1] = [−7/3] × [1/5] = −7/15
(ii) 5 ÷ (−7/3) = [5/1] × [3/−7] = 15/−7 = −2 (1/7)
(iii) −7/3 ÷ 35/62 = [−7/3] × [6/35] = −2/5

Try this
The closure property on integers holds for subtraction and not for division. What about rational numbers? Verify.
Solution:
Let 0 and 1/2 be two rational numbers 0 – 1/2 is a rational number
∴ Closure property for subtraction holds for rational numbers.
But consider the two rational number 5/2 and 0.
5/2 ÷ 0 = 5 / [2 × 0] = 5 / 0
Here denominator = 0 and it is not a rational number.
∴ Closure property is not true for division of rational numbers.
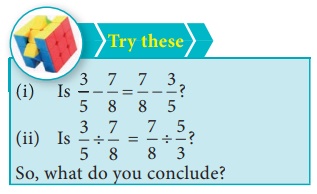
Solution:
Is 3/5 – 7/8 = 7/8 – 3/5 ?

LHS = 3/5 + 7/8 = [ (3 × 8) – (7 × 5) ] / 40 = [24 – 35] / 40 = −11/40
RHS = 7/8 − 3/5 = [ (7 × 5) – (3 × 8) ] / 40 = [35 – 24] / 40 = 11/40
LHS ≠ RHS
∴ 3/5 ÷ 7/8 ≠ 7/8 – 3/5
∴ Subtraction of rational numbers is not commutative.
(ii) Is 3/5 ÷ 7/8 = 7/8 – 5/3 ?

LHS = 3/5 ÷ 7/8 = 3/5 × 8/7 = 24/35
RHS = 7/8 ÷ 5/3 = 7/8 × 3/5 = 21/40
∴ LHS ≠ RHS
∴ 3/5 ÷ 7/8 ≠ 7/8 ÷ 5/3
∴ Commutative property not hold good for division of rational numbers.
Try this
Check whether associative property holds for subtraction and division.
Solution:

Consider the rational numbers 2/3, 1/2 and 3/4
To verify (2/3 – 1/2) – 3/4 = 2/3 – (1/2 – 3/4)
LHS = (2/3 – 1/2) – 3/4 = ( [(2 × 2) – (1 × 3)] / 6 ) – (3/4)
= ([4 – 3]/6) – 3/4 = 1/6 – 3/4 = [(1 × 2) – (3 × 3)] / 12 = [2 – 9] / 12 = – 7 / 12
RHS = 2/3 – (1/2 – 3/4) = 2/3 – ( [2 – 3] / 4) = ( 2/3 − (−1/4) )
= 2/3 + 1/4 = [ (2 × 4) + ( 1 × 3) ] / 12 = [ 8 + 3] / 12 = 11 / 12
LHS ≠ RHS
∴ ( 2/3 – 1/2) – 3/4 ≠ 2/3 − (1/2 − 3/4)
∴ Associative property not holds for subtraction of rational numbers
Also to verify (2/3 ÷ 1/2) ÷ 3/4 = 2/3 ÷ (1/2 ÷ 3/4)
LHS = (2/3 ÷ 1/2) ÷ 3/4 = (2/3 × 2/1) ÷ 3/4
= 4/3 ÷ 3/4 = 4/3 × 4/3 = 16 / 9
RHS = 2/3 ÷ (1/2 ÷ 3/4) = 2/3 ÷ ( 1/2 × 4/3) = 2/3 ÷ ( 2/3 )
= 2/3 × 3/2 = 1
LHS ≠ RHS
ie. (2/3 ÷ 1/2) ÷ 3/4 ≠ 2/3 ÷ ( 1/2 ÷ 3/4)
∴ Associative property does not hold for division of rational numbers.
Think
Observe that,
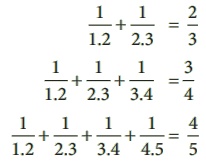
Use your reasoning skills, to find the sum of the first 7 numbers in the pattern given above.
Solution:
1/1.2 + 1/2.3 + 1/3.4 + 1/4.5 + 1/5.6 + 1/ 6.7 + 1/7.8 = 7 / 8
Think
1. Is the square of a prime number, prime?
Solution:
No, the square of a prime number ‘P’ has at least 3 divisors 1, P and P2. But a prime number is a number which has only two divisors, 1 and the number itself. So square of a prime number is not prime.
2. Will the sum of two perfect squares always be a perfect square? What about their difference and their product?
Solution:
The sum of two perfect squares, need not be always a perfect square. Also the difference of two perfect squares need not be always a perfect square. But the product of two perfect square is a perfect square.
Try these
• Which among 256, 576, 960, 1025, 4096 are perfect square numbers? (Hint: Try to extend the table of squares already seen).
Solution:
256 = 162
576 = 242
4096 = 642
∴ 256, 576 and 4096 are perfect squares
• One can judge just by look that each of the following numbers 82, 113, 1972, 2057, 8888, 24353 is not a perfect square. Explain why?
Solution:
Because the unit digit of a perfect square will be 0, 1, 4, 5, 6, 9. But the given numbers have unit digits 2, 3, 7, 8. So they are not perfect squares.
Think
Consider the claim: “Between the squares of the consecutive numbers n and (n+1), there are 2n non-square numbers”. Can it be true? How many non-square numbers are there between 2500 and 2601? Verify the claim.
Solution:
If n = 50 ⇒ n2 = 502 = 2500
n + 1 = 51 ⇒ (n + 1)2 = 512 = 2601
Non−square numbers of 2500 and 2601 = 100 = 2 × 50 = 2 n
So it is true that between the classes of successive numbers n, n + 1, there are non−square numbers of 2n.
Think
In this case, if we want to find the smallest factor with which we can multiply or divide 108 to get a square number, what should we do?
Solution:
108 = 2 × 2 × 3 × 3 = 22 × 32 × 3
If we multiply the factors by 2, then we get
22 × 32 × 3 × 3 ⇒ 22 × 32 × 32 = (2 × 3 × 3)2
Which is perfect square.
∴ Again if we divide by 3 then we get 22 × 32 ⇒ (2 × 3)2, a perfect square.
∴ We have to multiply or divide 108 by 3 to get a perfect square.
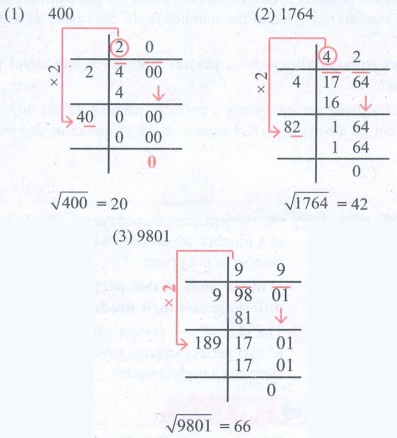
Try these
Find the square root by long division method.
1. 400 2. 1764 3. 9801
Solution:
Try these
Without calculating the square root, guess the number of digits in the square root of the following numbers:
1. 14400 2. 390625 3. 100000000
Solution:
(1) √14400 = √[144×100] = √l44 × √100
= 12 × 10 = 120.
(2) √390625 = √ [25 × 25 × 25 × 25]
= √[25×25] × √[25×25] = 25 × 25 = 625
(3) √100000000 = √[10000×10000]
= √10000 × √10000
= 100 × 100= 10,000
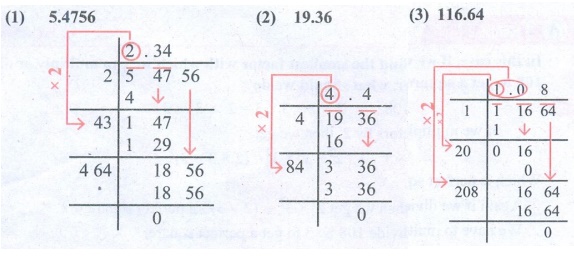
Try these
Find the s quare root of
1. 5.4756, 2. 19.36, 3. 116.64

Activity
Attempt to prepare a table of square root problems as in the above case to show that if a and b are two perfect square numbers, then √[a/b] = √a/√b (b ≠ 0). We can use this idea to compute certain square-root problems easily.
Try these
Using this method, find the square root of the numbers 1.2321 and 11.9025.
Solution:
(i) √1.2321 = √[12321/10000] = 111/100 = 1.11
(ii) √11.9025 = √119025 / √10000 = 345/100 = 3.45
Try these
Write the numbers in ascending order.
1. 4, √14 , 5
2. 7, √65 , 8
Solution:
(i) 4, √14, 5
Squaring all the numbers we get 42, (√l4)2, 52 ⇒ 16, 14, 25
∴ Ascending order : 14, 16, 25
Ascending order : √14, 4, 5
(ii) 7, √65, 8
Squaring 7, √65 and 8 we get 72, (√65)2 , 82 ⇒ 49, 65, 64
Ascending order : 49, 64, 65
Ascending order : 7, 8, √65
Try these
Find the ones digit in the cubes of each of the following numbers.
1. 12
2. 27
3. 38
4. 53
5. 71
6. 84
Solution:
(i) 12
12 ends with 2, so its cube ends with 8 i.e, ones digit in 123 is 8.
(2) 27
27 ends with 7, so its cube end with 3. i.e., ones digit in 273 is 3.
(3) 38
38 ends with 8, so its cube ends with 2 i.e, ones digit in 383 is 2.
(4) 53
53 ends with 3, so its cube ends with 7. i.e, ones digit in 533 is 7.
(5) 71
71 ends with 1, so its cube ends with 1. i.e, ones digit in 713 is 1
(6) 84
84 ends with 4, so its cube ends with 4. i.e, ones digit in 843 is 4.
Think
In this question, if the word ‘multiplied’ is replaced by the word ‘divided’, how will the solution vary?
Try these
Expand the following numbers using exponents:
1.8120 2. 20305 3. 3652.01 4. 9426.521
Solution:
(i) 8120 = (8 × 1000) + (1 × 100) + (2 × 10) + 0 × l
= (8 × 103) + (1 × 102) + (2 × 101)
(2) 20305 = (2 × 10000) + (0 × 1000) + (3 × 100) + ( 0 × 10) + (5 × 1)
= (2 × 104) + (3 × 102) + 5
(3) 3652.01 = 3000 + 600 + 50 + 2 + 0/10 + 1/100
= (3 × 1000) + (6 × 100) + (5 × 10) + (2 × 1) + 1 × 1/100)
= (3 × 103) + (6 × 102) + (5 × 101) + 2 + (1 × 10−2)
(4) 9426.521 = (9 × 1000) + (4 × 100) + (2 × 10) + (6 × 1) + (5/10) + (2/100) + (1/1000)
= (9 × 103) + (4 × 102) + (2 × 101) + 6 + (5 × 10−1) + (2 × 10−2) + (1 × 10−3)
Try these
Verify the following rules (as we did above). Here, a,b are non-zero integers and m, n are any integers.
1. Product of same powers to power of product rule: a m × b m = (ab)m
2. Quotient of same powers to power of quotient rule: an/bm = (a/b) m
3. Zero exponent rule: a0 = 1.
Verification:
Let a = 2; b = 3; m = 2
1. am × bm = 22 × 32 = 4 × 9 = 36 = (2 × 3)2
2. am / bm = 22 / 32 = 4 / 9 = (2 / 3)2
3. a0 = 20 = 1.
Try these
1. Write in standard form: Mass of planet Uranus is 8.68 × 1025 kg.
Solution:
Mass of Planet Uranus = 86800000000000000000000000 kg
2. Write in scientific notation: (i) 0.000012005 (ii) 4312.345 (iii) 0.10524 (iv)The distance between the Sun and the planet Saturn 1.4335×1012 miles.
Solution:
(i)  0.000012005 = 1.2005 × 10−5
0.000012005 = 1.2005 × 10−5
(ii) 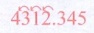 4312.345 = 4.312345 × 103
4312.345 = 4.312345 × 103
(iii) 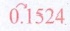 0.l 524 = 1.0524 × 10−1
0.l 524 = 1.0524 × 10−1
(iv) The distance between Sun and the planet Saturn is 1.4335 × 1012 miles
Note
The above examples show how a rational number may be given in decimal form. The reverse process of converting the decimal form of a rational number to the fractional form may be seen in the higher classes.
There are decimal numbers which are non-terminating and non-recurring such as
π = 3.141592653589793238462643…..
√2 = 1.41421356237309504880168……. etc.
They are not rational numbers and one can study more about them in the higher classes.
Note
0 is a rational number which is neither positive nor negative.
Note that −11/6 = 11/−6 = −11/6
Note
The collection of rational numbers is denoted by the letter ℚ because it is formed by considering all quotients, except those inv olving division by 0. Decimal numbers can be put in quotient form and hence they are also rational numbers.

Note:
We can find many rational numbers between – 7/11 and 5/-9 quickly as given below:
The range of rational numbers can be got by the cross multiplication of denominators with the numerators after writing the given fractions in standard form. The cross multiplication here 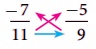 gives the range of rational numbers from –63 to –55 with the denominator 99. This is nothing but making the given rational numbers equivalent with the denominator 99!.
gives the range of rational numbers from –63 to –55 with the denominator 99. This is nothing but making the given rational numbers equivalent with the denominator 99!.


Note:
We know that different operations with the same pair of rational numbers usually give different answers. Check the following calculations which are some interesting exceptions in rational numbers.
(i) 13/4 + 13/9 = 13/4 × 13/9
(ii) 169/30 + 13/15 = 169/30 ÷ 13/15
Amazing …! Isn’t it? Try a few more like these, if possible.
Note
Perfect numbers such as 6, 28, 496, 8128 etc., are not square numbers.
Note
If a perfect square number ends in zero, then it must end with even number of zeroes always. We can verify this for a few numbers in the table given below.

Note
A perfect cube does not end with two zeroes.
The cube of a two digit number may have 4 or 5 or 6 digits in it.
Note
1. The positive exponent in 1.3 ×1012 indicates that it is a large number.
2. The negative exponent in 7.89 × 10–21 indicates that it is a small number.
Related Topics