Rational numbers between any two given rational numbers

Rational numbers between any two given rational numbers

Consider the integers 4 and 10. We can locate five integers namely 5,6,7,8 and 9 (shown in dark dots) between them. Isn’t it?

How many integers can you find between 3 and –2? List them.

Are there any integers between –5 and –4? No, is the answer.

This shows that the choice of integers between two given integers is limited. They are finite in number or may be nothing between them. Let us think what will happen, if we consider rational numbers instead of integers? We will see that we can have many rational numbers between any two rational numbers. There are at least two methods to find more rational numbers between any two rational numbers.

Method of Average

We know that that the average of any two numbers always lies at the middle of them.

For example, the average of 2 and 8 is 2 +8 / 2 = 5 and this 5 lies at the middle of 2 and 8 as shown in the following number line.

We use this idea to find more rational numbers between any two rational numbers.

Example 1.8

Find a rational number between 1/3 and 5/9.

Solution:

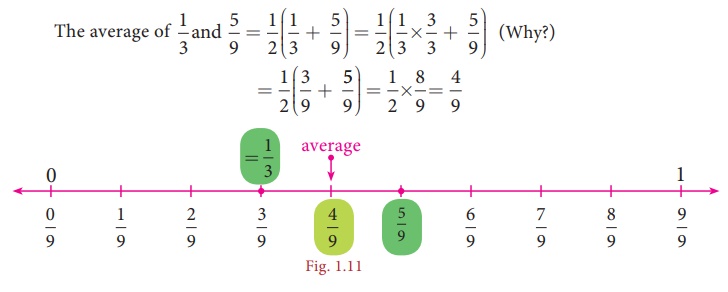
Note that 4/9 is one rational number we have found in between 1/3 and 5/9 and we can find many such numbers in between 1/3 and 5/9.This shows that between any two rational numbers there lie an unlimited number of rational numbers! Mathematically, we say that there lie an infinite number of rational numbers between any two rational numbers.

Think

Are there any rational numbers between −7/11 and 6/−11 ?

Solution:

−7/11 = −70/110 ; 6/−11 = −60/110

−61/110, −62/110 …. −69/110

∴ Thre are many rational numbers between −7/11 and 6/−11

Method of Equivalent rational numbers:

We can use the idea of equivalent fractions to get more rational numbers between any two rational numbers. This is clearly explained in the following illustration.

Illustration:

Let us now try to find more rational numbers say between 3/7 and 4/7 by the following visual explanation on the number line. If we get the multiples of the denominator of the equivalent rational numbers (the easy one will be to multiply by 10), then we can insert as many rational numbers as we want. We shall write 3/7 as 30/70 and 4/7 as 40/70 and see that there are 9 rational numbers between 3/7 and 4/7 as given in the number line below.

Now, if we want more rational numbers between say 37/70 and 38/70 we can write 37/70 as 370/700 and 38/70 as 380/700. Then again, we will get nine rational numbers between 37//70 and 38//70 as 371/700_, 372/700_, 373/700_, 374/700_, 375/700 _, 376/700_, 377/700 _, 378/700 and 379/700

The following diagram helps us to understand this nicely with a magnifying lens used between 0 and 1 and further zoomed into the fractional parts also

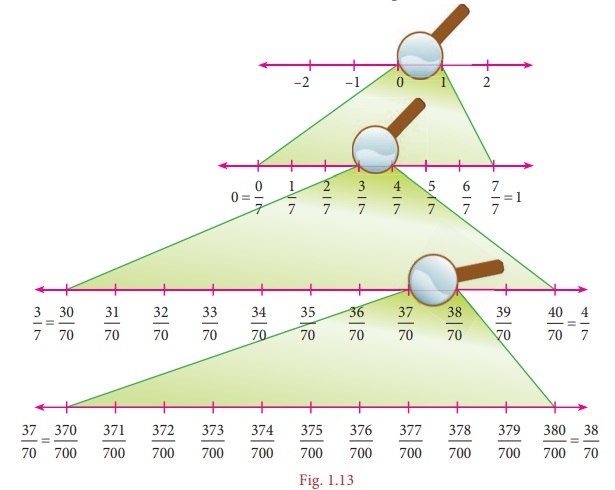
Thus, we can see that there are an unlimited number of rational numbers between any two given rational numbers.

Example 1.9

Find atleast two rational numbers between -3/4 and -2/5.

Solution:

The denominators are different for the given rational numbers. The LCM of the denominators 4 and 5 is 20. Make the rational numbers such that they have common denominators as 20. Here,

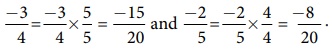
It is easy now to find and insert rational numbers between -15/20 and -8/20 and as shown below.

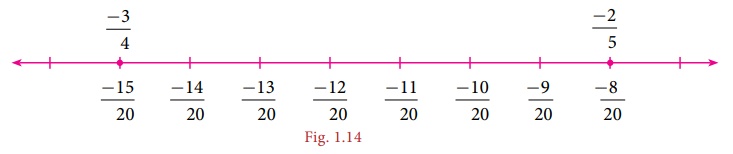
We can list a few rational numbers as 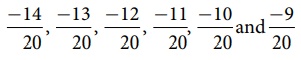 between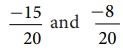 

Are these the only rational numbers between -15/20 and -8/20? Think! Try to find 10 more rational numbers between them, if possible!

Note:

We can find many rational numbers between – 7/11 and 5/-9 quickly as given below:

The range of rational numbers can be got by the cross multiplication of denominators with the numerators after writing the given fractions in standard form. The cross multiplication here 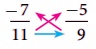 gives the range of rational numbers from –63 to –55 with the denominator 99. This is nothing but making the given rational numbers equivalent with the denominator 99!.