Summary

SUMMARY

• A number that can be expressed in the form a/b where a and b are integers and b ≠ 0 is called a rational number.

• All natural numbers, whole numbers, integers and fractions are rational numbers.

• Every rational number can be represented on a number line.

• 0 is neither a positive nor a negative rational number.

• A rational number a/b is said to be in the standard form if its denominator b is a positive integer and HCF (a,b) = 1

• There are unlimited numbers of rational numbers between two rational numbers.

• Subtracting two rational numbers is the same as adding the additive inverse of the second number to the first rational number.

• Multiplying two rational numbers is the same as multiplying their numerators and denominators separately and then writing the product in the standard form.

• Dividing a rational number by another rational number is the same as multiplying the first rational number by the reciprocal of the second rational number.

• The following table is about the properties of rational numbers (ℚ).

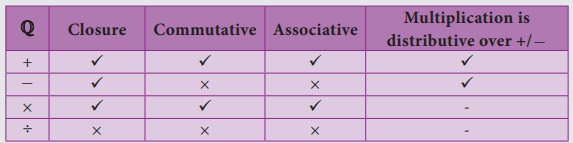
• 0 and 1 are respectively the additive and the multiplicative identities of rational numbers.

• The additive inverse for a/b is –a/b and vice – versa.

• The reciprocal or the multiplicative inverse of a rational number a/b is b/a since a/b × b/a = 1.

• A natural number n is called a square number, if we can find another natural number m such that n = m².

• The square root of a number n, written as √n (or) n^1/2 , is the number that gives n when multiplied by itself.

• The number of times a prime factor occurs in the square is equal to twice the number of times it occurs in the prime factorization of the number.

• For any two positive numbers a and b. we have

(i) √ab = √a × √b and (ii) √(a/b) = √a/√b (b≠0)

• If you multiply a number by itself and then by itself again, the result is a cube number.

• The cube root of a number is the value that when cubed gives the original number.

• An expression that represents repeated multiplication of the same factor is called a power.

• The exponent corresponds to the number of times the base is used as a factor.

• Laws of Exponents: (i) a^m × aⁿ = a^m + n (ii) a^m / aⁿ = a^m-n (iii) (a^m)ⁿ = a^mn

• Other results: (i) a⁰ = 1 (ii) a^−m = 1/a^m (iii) a^m × b^m = (ab)^m (iv) a^m/b^m = (a/b^)m

• To write in scientific notation, we follow the form S × 10^a where S is a number (integer or integer with decimal) between 1 and 10, but not 10 itself, and a is a positive or negative integer.