Properties of Rational Numbers

Properties of Rational Numbers

Some properties listed here below will be of good use in solving problems.

1. Closure property/law for the collection ℚ of rational numbers

i) Closure property for Addition

For any two rational numbers a and b, the sum a + b is also a rational number.

ii) Closure property for Multiplication

For any two rational numbers a and b, the product ab is also a rational number.

Illustration

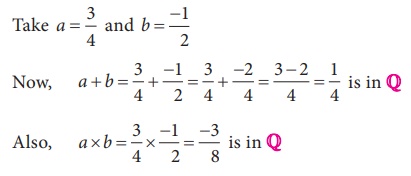
Try this

The closure property on integers holds for subtraction and not for division. What about rational numbers? Verify.

Solution:

Let 0 and 1/2 be two rational numbers 0 – 1/2 is a rational number

∴ Closure property for subtraction holds for rational numbers.

But consider the two rational number 5/2 and 0.

5/2  ÷ 0 = 5 / [2 × 0] = 5 / 0

Here denominator = 0 and it is not a rational number.

∴ Closure property is not true for division of rational numbers. 

2. Commutative property/law for the collection ℚ of rational numbers

i) Commutative property for Addition

For any two rational numbers a and b, a + b = b + a.

ii) Commutative property for Multiplication

For any two rational numbers a and b, ab = ba (ab means a × b and ba means b × a).

Illustration

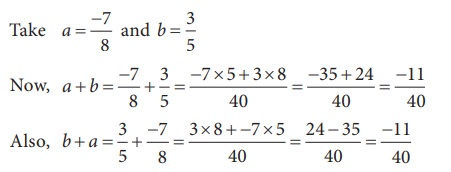
Here, we find that a + b = b + a and hence addition is commutative.

Further,

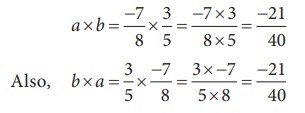
Here, we find that a × b = b × a and hence multiplication is commutative

Solution:

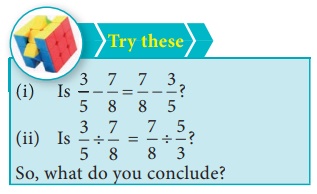
Is 3/5 – 7/8 = 7/8 – 3/5 ?

LHS = 3/5 + 7/8 = [ (3 × 8) – (7 × 5) ] / 40 = [24 – 35] / 40 = −11/40

RHS = 7/8 − 3/5 = [ (7 × 5) – (3 × 8) ] / 40 = [35 – 24] / 40 = 11/40

LHS  ≠  RHS

∴ 3/5  ÷ 7/8  ≠ 7/8 – 3/5

∴ Subtraction of rational numbers is not commutative.

(ii) Is 3/5 ÷ 7/8 = 7/8 – 5/3 ?

LHS = 3/5  ÷  7/8 = 3/5  × 8/7 = 24/35

RHS = 7/8  ÷  5/3 = 7/8  × 3/5 = 21/40

∴ LHS  ≠  RHS

∴ 3/5  ÷ 7/8  ≠ 7/8 ÷ 5/3

∴ Commutative property not hold good for division of rational numbers.

3. Associative property/law for the collection ℚ of rational numbers

i) Associative property for Addition

For any three rational numbers a, b, and c, a + (b + c) = (a + b) + c

ii) Associative property for Multiplication

For any three rational numbers a, b, and c, a(bc) = (ab)c

Illustration

Take rational numbers a , b, c as a = −1/2 , b = 3/5 and c = −7/10

(3) and (4) shows that

 (a × b) × c = a × (b × c) is true for rational numbers. Thus, the associative property is true for addition and multiplication of rational numbers.

Try this

 Check whether associative property holds for subtraction and division.

Solution:

Consider the rational numbers 2/3, 1/2  and 3/4

To verify (2/3 – 1/2) – 3/4 = 2/3 – (1/2 – 3/4)

LHS = (2/3 – 1/2) – 3/4 = ( [(2 × 2) – (1 × 3)] / 6 ) – (3/4)

= ([4 – 3]/6) – 3/4 = 1/6 – 3/4 = [(1 × 2) – (3 × 3)] / 12 = [2 – 9] / 12 = – 7 / 12

RHS = 2/3 – (1/2 – 3/4) = 2/3 – ( [2 – 3] / 4) =  ( 2/3 −  (−1/4) )

= 2/3 + 1/4  = [ (2 × 4) + ( 1 × 3) ] / 12 = [ 8 + 3] / 12 = 11 / 12

LHS  ≠  RHS

∴ ( 2/3 – 1/2) – 3/4  ≠ 2/3  − (1/2 − 3/4)

∴ Associative property not holds for subtraction of rational numbers

Also to verify (2/3 ÷ 1/2) ÷ 3/4 = 2/3 ÷ (1/2 ÷ 3/4)

LHS = (2/3  ÷  1/2) ÷  3/4 = (2/3 × 2/1) ÷ 3/4

= 4/3  ÷ 3/4 = 4/3 × 4/3 = 16 / 9

RHS = 2/3 ÷ (1/2 ÷ 3/4) = 2/3 ÷ ( 1/2 × 4/3) =  2/3 ÷  ( 2/3 )

= 2/3 × 3/2 = 1

LHS  ≠  RHS

ie. (2/3 ÷ 1/2) ÷ 3/4 ≠ 2/3 ÷ ( 1/2 ÷ 3/4)

∴ Associative property does not hold for division of rational numbers.

4. Identity property/law for the collection ℚ of rational numbers

i) Identity property for Addition

For any rational number a, there exists a unique rational number 0 such that

0 + a = a = 0 + a.

ii) Identity property for Multiplication

For any rational number a, there exists a unique rational number 1 such that

1 × a = a = a × 1.

Illustration

Take a = 3/-7 that is, a = -3/7 . Now -3/7 + 0 = -3/7 = 0 + -3/7 (Isn’t it?)

Hence, 0 is the additive identity for −3/7

Also, -3/7 × 1 = - 3/7 = 1 × -3/7 (Isn’t it?)

Hence, 1 is the multiplicative identity for −3/7

5. Inverse property/law for the collection ℚ of rational numbers

i) Additive Inverse property

For any rational number a, there exists a unique rational number –a such that a + (–a) = (–a) + a = 0. Here, 0 is the additive identity.

ii) Multiplicative Inverse property

For any rational number b, there exists a unique rational number 1/b such that b × 1/ b = 1/b × b = 1 . Here, 1 is the multiplicative identity.

Illustration

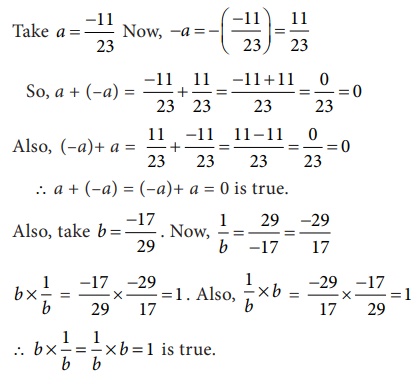
6. Distributive property/law for the collection ℚ of rational numbers

Multiplication is distributive over addition for the collection of rational numbers. For any three rational numbers a, b and c, the distributive law is a × (b +c) = ( a × b) +(a × c)

Illustration

 (1) and (2) shows that a × (b + c ) = (a × b) + (a × c) .

Hence, multiplication is distributive over addition for the collection ℚ of rational numbers.