Exercise 1.4 (Square Root)

Exercise 1.4

1. Fill in the blanks:

(i) The ones digit in the square of 77 is___________. [Answer: 9]

(ii) The number of non-square numbers between 24² and 25² is ______. [Answer: 48]

(iii) The number of perfect square numbers between 300 and 500 is ______. [Answer: 5]

(iv) If a number has 5 or 6 digits in it, then its square root will have ___________ digits. [Answer: 3]

(v) The value of √180 lies between integers ______ and ______. [Answer: 13, 14]

2. Say True or False:

(i) When a square number ends in 6, its square root will have 6 in the unit’s place. [Answer: True]

(ii) A square number will not have odd number of zeros at the end. [Answer: True]

(iii) The number of zeros in the square of 91000 is 9. [Answer: False]

(iv) The square of 75 is 4925. [Answer: False]

(v) The square root of 225 is 15. [Answer: True]

3. Find the square of the following numbers.

(i) 17 (ii) 203 (iii) 1098

Solution:

4. Examine if each of the following is a perfect square.

(i) 725 (ii) 190 (iii) 841 (iv) 1089

(i) 725 (ii) 190 (iii) 841 (iv) 1089

Solution:

(i) 725

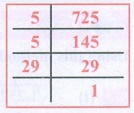
725 = 5 × 5 × 29 = 5² × 29

Here the second prime factor 29 does not have a pair.

Hence 725 is not a perfect square number.

(ii) 190

190 = 2 × 5 × 19

Here the factors 2, 5 and 9 does not have pairs.

Hence 190 is not a perfect square number.

(iii) 841

841 = 29 × 29

Hence 841 is a perfect square

(iv) 1089

1089 = 3 × 3 × 11 × 11

1089 = 3² × 11²

√1089 = 3 × 11 = 33

Hence 1089 is a perfect square

5. Find the square root by prime factorisation method.

(i) 144 (ii) 256 (iii) 784 (iv) 1156 (v) 4761 (vi) 9025

Solution:

(i) 144

144 = 2 × 2 × 2 × 2 × 3 × 3

√l44 = 2 × 2 × 3 = 12

(ii) 256

256 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2

√256 = 2 × 2 × 2 × 2 = 16

(iii) 784

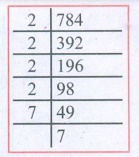
784 = 2 × 2 × 2 × 2 × 7 × 7

√784 = 2 × 2 × 2 × 2 × 7 × 7 = 28

(iv) 1156

1156 = 2 × 2 × 17 × 17

1156 = 2² × 17²

1156 = (2 × 17)²

∴ √1156 = √(2 × l7)² = 2 × 17 = 34

√1156 = 34

 (v) 4761

4761 = 3 × 3 × 23 × 23

4761 = 3² × 23²

4761 = (3 × 23)²

√4761 = √(3 × 23)²

√4761 = 3 × 23

√4761 = 69

(vi) 9025

9025 = 5 × 5 × 19 × 19

9025 = 5² × 19²

9025  = (5 × 19)²

√925 = = √ (5 × 19)² = 5 × 19 = 95

6. Find the square root by long division method.

(i) 1764 (ii) 6889 (iii) 11025 (iv) 17956 (v) 418609

Solution:

7. Estimate the value of the following square roots to the nearest whole number:

(i) √440 (ii) √800 (iii) √1020

Solution:

(i) √440

We have 20² = 400

 21² = 441

 ∴ √440 ≃ 21

(ii) √800

We have 28² = 784

 29² = 841

∴ √800 ≃ 28

(iii) √1020

We have 31² = 961

 32² = 1024

∴ √1020 ≃ 32.

8. Find the square root of the following decimal numbers and fractions.

(i) 2.89 (ii) 67.24 (iii) 2.0164 (iv) 144/225 (v) 

Solution:

(i) 2.89

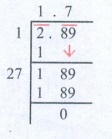
√2.89 = 1.7

(ii) 67.24

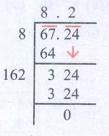
√67.24 = 8.2

(iii) 2.0164

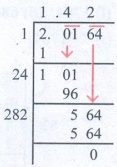
√2.0164 = 1.42

(iv) 144/225 = √[144/225] = 12/15

(v) 7 (18/49) = √[361/49] = √361/√49 = √19²/√7² =19/7

9. Find the least number that must be subtracted to 6666 so that it becomes a perfect square. Also, find the square root of the perfect square thus obtained.

Solution:

Let us work out the process of finding the square root of 6666 by long division method.

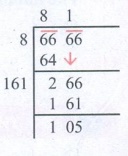
The remainder in the last step is 105. Is if 105 be subtracted from the given number the remainder will be zero and the new number will be a perfect square.

∴ The required number is 105. The square number is 6666 − 105 = 6561.

∴ √6561 = 81

10. Find the least number by which 1800 should be multiplied so that it becomes a perfect square. Also, find the square root of the perfect square thus obtained.

Solution:

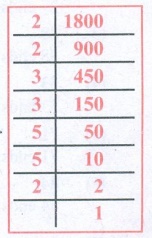
We find 1800 = 2 × 2 × 3 × 3 × 5 × 5 × 2

= 2² × 3² × 5² × 2

Here the last factor 2 has no pair. So if we multiply

1800 by 2, then the number becomes a perfect square.

∴ 1800 × 2 = 3600 is the required perfect square number.

∴ 3600 = 1800 × 2

3600 = 2² × 3² × 5² × 2 × 2

3600 = 2² × 3² × 5² × 2²

= (2 × 3 × 5 × 2)²

√3600 = √(2 × 3 × 5 × 2)²

= 2 × 3 × 5 × 2 = 60

∴ √3600 = 60.

Objective Type Questions

11. The square of 43 ends with the digit ______.

(A) 9

(B) 6

(C) 4

(D) 3

[Answer: (A) 9]

Solution: Ones digit = 3 × 3 = 9

12. _______ is added to 24² to get 25².

(A) 4²

(B) 5²

(C) 6²

(D) 7²

[Answer: (A) 7²]

Solution:

25² = 25 × 25 = 625

24² = 24 × 24 = 576

625 −576 = 49

49 = 7²

13. √48 is approximately equal to ______.

(A) 5

(B) 6

(C) 7

(D) 8

[Answer: (C) 7]

Solution: √49 = 7

14. √128 - √98 + √18 = ______.

(A) √2

(B) √8

(C) √48

(D) √32

[Answer: (D) √32]

15. The number of digits in the square root of 123454321 is ______.

(A) 4

(B) 5

(C) 6

(D) 7

[Answer: (B) 5]

Solution:

= [n + 1] / 2 = 10/2 = 5

Answer:

Exercise 1.4

1. (i) 9 (ii) 48 (iii) 5 (iv) 3 (v) 13, 14

2. (i) True (ii) True (iii) False (iv) False (v) True

3. (i) 289 (ii) 41209 (iii) 1205604

4. (i) No (ii) No (iii) Yes (iv) Yes

5. (i) 12 (ii) 16 (iii) 28 (iv) 34 (v) 69 (vi) 95

6. (i) 42 (ii) 83 (iii) 105 (iv) 134 (v) 647

7. (i) 21 (ii) 28 (iii) 32

8. (i) 1.7 (ii) 8.2 (iii) 1.42 (iv) 12/15 (v) 2 5/7

9. 105, 81 10. 2, 60

11. (A) 9

12. (D) 7²

13. (C) 7

14. (D) √32

15. (B) 5