Rational numbers in Standard form

Rational numbers in Standard form

Observe the following rational numbers: 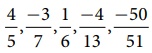. Here, we see that

i) the denominators of these rational numbers are all positive integers

ii) 1 is the only common factor between the numerator and the denominator of each of them and

iii) the negative sign occurs only in the numerator.

Such rational numbers are said to be in standard form.

A rational number is said to be in standard form, if its denominator is a positive integer and both the numerator and denominator have no common factor other than 1.

If a rational number is not in the standard form, then it can be simplified to arrive at the standard form.

The collection of rational numbers is denoted by the letter ℚ because it is formed by considering all quotients, except those inv olving division by 0. Decimal numbers can be put in quotient form and hence they are also rational numbers.

Example 1.2

Reduce to the standard form: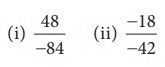 

Solution:

(i) Method 1:

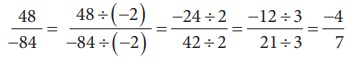 (dividing by –2,2 and 3 successively)

Method 2:

The HCF of 48 and 84 is 12 (Find it!). Thus, we can get its standard form by dividing it by –12.

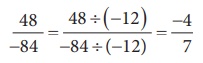
(ii) Method 1:

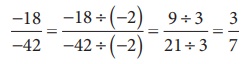
(dividing by –2 and 3 successively)

Method 2:

The HCF of 18 and 42 is 6 (Find it!). Thus, we can get its standard form by dividing it by 6.

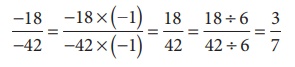
Try these

1. Which of the following pairs represents equivalent rational numbers?

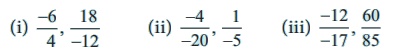
(i) −6/4, 18/−12

 −6/4 = [−6 × 3] / [4 × 3] = −18 / 12

∴  −6 / 4 = equivalent to −18 / 12

(ii) −4/−20, 1/−5

−4/−20 = [−4 ÷ (−4)] / [−20 ÷ (−4)] = 1/5 ≠ −1/5

∴ −4 / −20  not equivalent to 1 / −5

(iii) −12/−17, 60/85

−12 / −17 = [−12 × −5] / [−17 × −5] = 60 / 85

∴ −12 / −17 equivalent to 60 / 85

2. Find the standard form of:

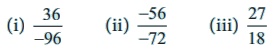
(i) 36/−96  = [−36 ÷ 12] / [96 ÷ 12] = −3 / 8

(ii) −56/−72 = [−56  ÷ (−8)] / [−72  ÷ (−8)] = 7 / 9

(iii) 27/18 = 1 (9/18) = 1 (1/2)

3. Mark the following rational numbers on a number line.

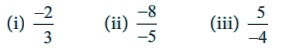
Solution:

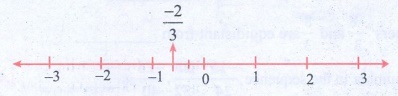
(i) −2 / 3

−2/3 lies between 0 and −1.

The unit part between 0 and −1 is divided into 3 equal parts and second part taken.

(ii) −8 / −5

−8/−5 = 1 (3/5)

1 (3/5) lies between 1 and 2. The unit part between 1 and 2 is divided into 5 equal parts and the third part is taken.

(iii) 5 / −4

 5 / −4 = − 5/4 = − 1 ¼

−1 (1/4) lies between −1 and −2. The unit part between −1 and −2 is divided into four equal parts and the first part is taken.