Exercise 1.6 (Exponents and Powers)

Exercise 1.6

1. Fill in the blanks:

(i) (−1)^{even integer} is _____________. [Answer:1]

(ii) For a ≠ 0, a⁰ is ______________. [Answer:1]

(iii) 4^-3 × 5^-3 __________. [Answer:20⁻³]

(iv) (-2)^-7 = ____________. [Answer:−1/128]

(v) (-1/3)^-5 = ____________. [Answer: −243]

2. Say True or False:

(i) If 8^x = 1/64, the value of x is − 2. [Answer: True]

(ii) The simplified form of (256)^−1/4 × 4² is ¼. [Answer: False]

(iii) Using the power rule, (3⁷)^-2 = 3⁵. [Answer: False]

(iv) The standard form of 2 × 10^–4 is 0.0002. [Answer: True]

(v) The scientific form of 123.456 is 1.23456×10⁻². [Answer: False]

3. Evaluate: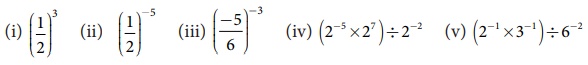 

(i) (1/2)³

Solution:

(1/2)³ = 1³/2³ = 1 / [2 × 2 × 2] = 1 / 8

(ii) (1/2)⁻⁵.

Solution:

(1/2)⁻⁵ = 1⁻⁵ / 2⁻⁵ = 1 / 2⁻⁵ = 2⁵ = 2 × 2 × 2 × 2 × 2 = 32

(iii) (−5/6)⁻³

Solution:

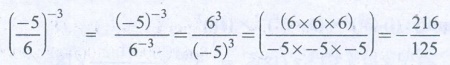
(−5/6)⁻³ = (−5)⁻³ / 6⁻³ = 6³ / (−5)⁻³ = ( (6 × 6 × 6) / (−5 × −5 × −5) ) = − 216/125

(iv) (2⁻⁵ × 2⁷) ÷ 2⁻²

Solution:

(2⁻⁵ × 2⁷) ÷ 2⁻² = (2⁻⁵⁺⁷) ÷ 2⁻²

= 2² ÷ 2⁻²

= 2²⁺²

= 2⁴ = 16

(v) (2⁻¹ × 3⁻¹) ÷ 6⁻²

Solution:

(2⁻¹ × 3⁻¹) ÷ 6⁻² = (2 × 3)⁻¹ ÷ 6⁻²

= (6)⁻¹ ÷ 6⁻²

= (6)^{−1 – (−2)} = 6¹ = 6

4. Evaluate: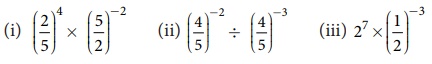 

Solution:

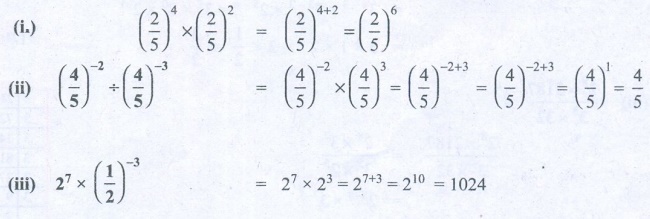
(2/5)⁴ × (2/5)² = (2/5)⁴⁺²  =  (2/5)⁶

(ii) (4/5)⁻² ÷ (4/5)⁻³ = (4/5)⁻² × (4/5)³  = (4/5)⁻²⁺³  = (4/5)⁻²⁺³  = (4/5)¹ = 4/5

(iii) 2⁷ × (1/2)⁻³ = 2⁷ × 2³ = 2⁷⁺³ = 2¹⁰ = 1024

5. Evaluate: (i) (5⁰ +6^-1) × 3² (ii) (2^-1 + 3^-1 ) ÷ 6^-1 (iii) ( 3^-1 + 4^-2 + 5^-3)⁰

Solution:

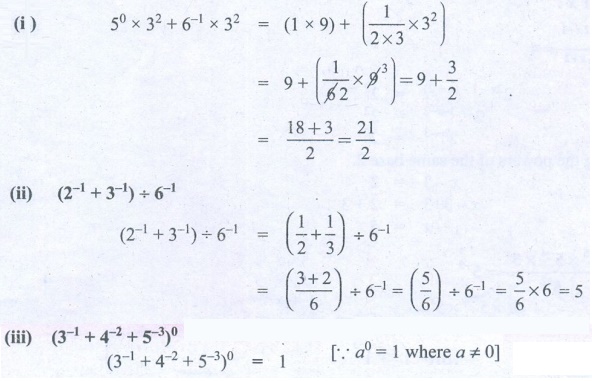
 (i) (5⁰ +6⁻¹) × 3²

5⁰ × 3² + 6⁻¹ × 3² = (1 × 9) + ( {1 / [2×3]} × 3²)

= 9 + ( 1/6 × 9 ) = 9 + 3/2

= [18 + 3] / 2 = 21/2

(ii) (2⁻¹ + 3⁻¹) ÷ 6⁻¹

 (2⁻¹ + 3⁻¹) ÷ 6⁻¹ = (1/2 + 1/3) ÷ 6⁻¹

= ( [3 + 2] / 6) ÷ 6⁻¹  = (5/6) ÷ 6⁻¹ = 5/6 × 6 = 5

(iii) (3⁻¹ + 4⁻² + 5⁻³)⁰

 (3⁻¹ + 4⁻² + 5⁻³)⁰ = 1

[∵  a⁰ = 1 where a ≠ 0]

6. Simplify: (i) (3²)³ × (2×3⁵)^–2 × (18)²

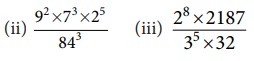
Solution:

(i) (3²)³ × (2 × 3⁵)⁻² × (18)²

(3²)³ × (2 × 3⁵)⁻² × (18)² = 3^2x3 × [1 / (2 × 3⁵)² ] × 18²

= 3⁶ × [1 / 2²×(3⁵)² ] × 18² = 3⁶  × [ 1 / 2²×3¹⁰ ] × (2×3²)²

= 3⁶  × [ 1 / 2²×3¹⁰ ] × 2² × 3^2×2 =  3⁶ × [ 1 / 2²×3¹⁰ ] × 2² × 3⁴

= [3⁶⁺⁴  × 2² ] / [2² × 3¹⁰ ] = [3¹⁰ × 2² ] / [ 2² × 3¹⁰ ] = 1

(ii) [ 9² × 7³ × 2⁵ ] / 84³

[ 9² × 7³ × 2⁵ ] / 84³ = [ (3²)² × 7³ × 2⁵ ] / [ (2² × 3 × 7)³ ] = [ 3^2x2 × 7³ × 2⁵ ] / [ 2^2x3x 3³ × 7³ ] = [ 3^{4 ×} 7³ × 2⁵ ] / [ 2^{6 ×} 3³ × 7³ ]

= 3⁴⁻³ × 7³⁻³ × 2⁵⁻⁶ = 3¹ × 7⁰ × 2⁻¹

= 3 × 1 × 2⁻¹ = 3 × (1/2) = 3/2

(iii) [ 2⁸ × 2187] / [3⁵ × 32]

Solution:

[2⁸ × 2187] / [3⁵ × 32] = [2⁸ × 3⁷ ] / [ 3⁵ × 2⁵]

= 2⁸⁻⁵ × 3⁷⁻⁵

= 2³ × 3² = 8 × 9 = 72 

7. Solve for x: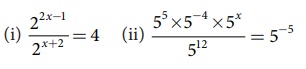 

(i) 2^2x−1 / 2^x+2 = 4

Solution:

2^{2x−1 –(x+2)} = 2²

2^{2x−1 –x−2)} = 2²

2^x−3 = 2²

Equating the powers of the same base 2.

x−3 = 2

x – 3 + 3 = 2 + 3

x = 5

(ii) [ 5⁵ × 5⁻⁴ × 5^x ] / 5¹² = 5⁻⁵

[ 5⁵ × 5⁻⁴ × 5^x ] / 5¹² = 5⁻⁵

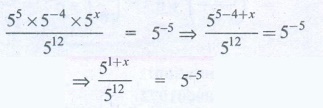
⇒ [ 5^{5 −4 + x} ] / 5¹² = 5⁻⁵

⇒ 5^{1+ x} / 5¹² = 5⁻⁵

⇒ 5^{1+ x − 12} = 5⁻⁵

⇒ 5 ^{x −11} = 5⁻⁵

Equating the powers of same base 5.

x − 11 = −5

x —11 + 11 = −5 + 11

x = 6

8. Expand using exponents: (i) 6054.321 (ii) 897.14

(i) 6054.321 = (6 × 1000) + (0 × 100) + (5 × 10) + (4 × 10⁰) + 3/10 + 2/100 + 1/1000

= (6 × 10³) + (5 × l0¹) + (4 × 10⁰) + ( 3 × 1/10) + ( 2 × 1/100) + (1 × 1/1000)

= (6 × 10³) + (5 × l0¹) + (4 × 10⁰) + ( 3 × 10⁻¹) + ( 2 × 10⁻²) + (1 × 10⁻³)

(ii) 897.14 = (8 × 100) + (9 × 10) + (7 × 10⁰) + l/10 + 4/100

=  (8 × 10²) + (9 × 10¹) + (7 × 10⁰) + (l × 1/10) + (4 × 1/100)

=  (8 × 10²) + (9 × 10¹) + (7 × 10⁰) + (l × 10⁻¹) + (4 × 10⁻²)

9. Find the number in standard form for the following expansions:

(i) 8×10⁴ +7×10³ +6×10² +5×10¹ +2×1+ 4×10^-2 +7×10^-4

(ii) 5×10³ + 5×10¹ + 5×10^–1 + 5 ×10^–3

(iii) The radius of a hydrogen atom is 2.5 × 10^–11 m

Solution:

(i) 8 × 10⁴ + 7 × 10³ + 6 × 10²  + 5 × 10¹ + 2 × 1 + 4 × 10⁻² + 7 × 10⁻⁴

  (8 × 10⁴) + (7 × 10³) + (6 × 10²)  + (5 × 10¹) + (2 × 1) + (4 × 10⁻²) + (7 × 10⁻⁴)

= (8 × 10000) + (7 × 1000) + (6 × 100) + (5 × 10) + (2 × 1) + (4 × 1/100) + (7 × 1/10000)

= 80000 + 7000 + 600 + 50 + 2 + (4/100) + (7/10000)

= 87652.0407

(ii) 5 × 10³ + 5 × 10¹ + 5 × 10⁻¹ + 5 × 10⁻³

Solution:

5 × 10³ + 5 × 10¹ + 5 × 10⁻¹ + 5 × 10⁻³

= 5 × 1000 + 5 × 10 + 5 × 1/10 + 5 × 1/1000

= 5000 + 50 + 5/10 + 5/1000 = 5050.505

(iii) The radius of a hydrogen atom is 2.5 × 10⁻¹¹ m.

Solution:

Radius of a hydrogen atom = 2.5 × 10⁻¹¹ m

= 2.5 × 1/10¹¹ m = 2.5/10¹¹m = 0.000000000025 m

10. Write the following numbers in scientific notation:

(i) 467800000000 (ii) 0.000001972 (iii) 1642.398

(iv) Earth’s volume is about 1,083,000,000,000 cubic kilometres

(v) If you fill a bucket with dirt, the portion of the whole Earth that is in the bucket will be 0.0000000000000000000000016 kg

Solution:

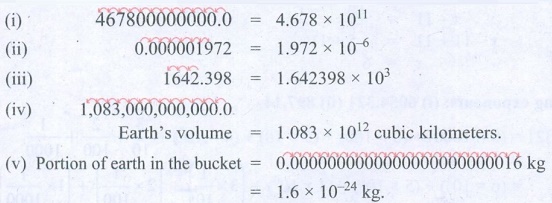
Objective Type Questions

11. By what number should (−4)⁻¹ be multiplied so that the product becomes 10^-1 ?

(A) 2/3

(B) −2/5

(C) 5/2

(D) −5/2

[Answer: (B) −2/5]

Solution:

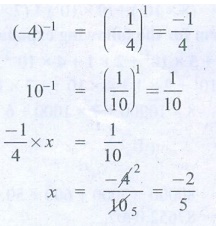
(−4)⁻¹ = (−1/4)¹ = −1/4

10⁻¹ = (1/10)¹ = 1/10

(−1/4) × x = 1/10

x = −4 / 10 = −2 / 5

12. (−2)⁻³ × (−2 )⁻² = ____________.

(A) −1/32

(B) 1/32

(C) 32

(D) –32

[Answer: (A) −1/32]

13. Which is not correct?

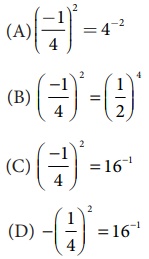
[Answer: (D) –(1/4)² = 16⁻¹]

Solution:

(−2) – 3x( − 2) – 2 = (−2) – 3 – 2 = (−2) −5 (−1/2)5 = −1/32

14. If 10^x/10^-3 =10⁹ ,then x is ____________.

(A) 4

(B) 5

(C) 6

(D) 7

[Answer: (C) 6]

15. 0.0000000002020 in scientific form is ____________.

(A) 2.02×10⁹

(B) 2.02×10⁻⁹

(C) 2.02×10⁻⁸

(D) 2.02×10⁻¹⁰

[Answer: (D) 2.02 × l0−10]

Solution: 

Answer

Exercise 1.6

1. (i) 1 (ii) 1 (iii) 20⁻³ (iv) −1/128 (v) –243

2. (i) True  (ii) False  (iii) False  (iv) True  (v) False

3. (i) 1/8  (ii) 32  (iii) – 216/125  (iv) 16  (v) 6

4. (i) 64/15625  (ii) 4/5  (iii) 1024 

5. (i) 21/2 (ii) 5 (iii) 1

6. (i) 1  (ii) 3/2  (iii) 72 

7. (i) x = 5  (ii) x = 6

8. (i) 6 × 10³ + 5 × 10¹ + 4 × 10⁰ + 3 × 10^‒1 + 2 × 10^‒2 + 1 × 10^-3

(ii) 8 × 10² + 9 × 10¹ + 7 × 10⁰ + 1 × 10^‒1 + 4 × 10^‒2

9. (i) 87652.0407 (ii) 5050.505 (iii) 0.000000000025

10. (i) 4.678 × 10¹¹ (ii) 1.972 × 10^‒6 (iii) 1.642398 ×10³ (iv) 1.083 ×10¹² cu. km (v) 1.6 ×10^‒24

11. (B)  -2/5

12. (A)  -1/32

13. (D) – (1/4)² = 16^-1  

14. (C) 6 

15. (D) 2.02×10^-10