Introduction to Square Numbers

Introduction to Square Numbers

More often we write like this:

4²=16

This says “4 squared is 16”

The 2 at the top stands for squared and it indicates the number of times the number 4 appears in the product (4² = 4 × 4 = 16).

The numbers 1, 4, 9, 16, ... are all square numbers (also called perfect square numbers).

Each of them is made up of the product of same two factors.

A natural number n is called a square number, if we can find another natural number m such that n = m².

Is 49 a square number? Yes, because it can be written as 7². Is 50 a square number?

The following table gives the squares of numbers up to 20.

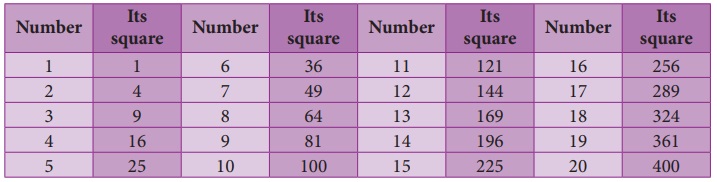
Try to extend the table up to 50 numbers!

We can now easily verify the following properties of square numbers by referring the table given above:

• The square numbers end with 0, 1, 4, 5, 6 and 9 only.

• If a number ends with 1 or 9, its square ends with 1.

• If a number ends with 2 or 8, its square ends with 4.

• If a number ends with 3 or 7, its square ends with 9.

• If a number ends with 4 or 6, its square ends with 6.

• If a number ends with 5 or 0, its square also ends with 5 or 0 respectively.

• Square of an odd number is always odd and the square of an even number is always even.

• Numbers that end with 2,3,7 and 8 are not perfect squares.

Think

1. Is the square of a prime number, prime?

Solution:

No, the square of a prime number ‘P’ has at least 3 divisors 1, P and P². But a prime number is a number which has only two divisors, 1 and the number itself. So square of a prime number is not prime.

2. Will the sum of two perfect squares always be a perfect square? What about their difference and their product?

Solution:

The sum of two perfect squares, need not be always a perfect square. Also the difference of two perfect squares need not be always a perfect square. But the product of two perfect square is a perfect square.

Try these

• Which among 256, 576, 960, 1025, 4096 are perfect square numbers? (Hint: Try to extend the table of squares already seen).

Solution:

256 = 16²

576 = 24²

4096 = 64²

∴ 256, 576 and 4096 are perfect squares

• One can judge just by look that each of the following numbers 82, 113, 1972, 2057, 8888, 24353 is not a perfect square. Explain why?

Solution:

Because the unit digit of a perfect square will be 0, 1, 4, 5, 6, 9. But the given numbers have unit digits 2, 3, 7, 8. So they are not perfect squares.

1. Some more special properties of square numbers

(i) The square of a natural number other than 1, is either a multiple of 3 or exceeds a multiple of 3 by 1.

(ii) The square of a natural number, other than 1, is either a multiple of 4 or exceeds a multiple of 4 by 1.

(iii) Th e remainder of a perfect square when divided by 3, is either 0 or 1 but never 2.

(iv) Th e remainder of a perfect square, when divided by 4, is either 0 or 1 but never 2 and 3.

(v) When a perfect square number is divided by 8, the remainder is either 0 or 1 or 4, but will never be equal to 2, 3, 5, 6 or 7.

Perfect numbers such as 6, 28, 496, 8128 etc., are not square numbers.

Note

If a perfect square number ends in zero, then it must end with even number of zeroes always. We can verify this for a few numbers in the table given below.

Example 1.22

Th e area of a square field is 3136 m². Find its perimeter.

Solution:

Given that the area of the square field = 3136 m²

∴The side of square field = √3136 m= 56 m

∴The perimeter of the square fi eld = 4 × side

= 4 × 56

= 224 m

Think

Consider the claim: “Between the squares of the consecutive numbers n and (n+1), there are 2n non-square numbers”. Can it be true? How many non-square numbers are there between 2500 and 2601? Verify the claim.

Solution:

 If n = 50 ⇒ n² = 50² = 2500

n + 1 = 51 ⇒ (n + 1)² = 51² = 2601

Non−square numbers of 2500 and 2601 = 100 = 2 × 50 = 2 n

So it is true that between the classes of successive numbers n, n + 1, there are non−square numbers of 2n.

Example 1.23

A real estate owner had two plots, a square plot of side 39 m and a rectangular plot of dimensions 100 m length and 64 m breadth. He sells both of these plots and acquires a new square plot of the same area. What is the length of side of his new plot?

Solution:

The transactions can be visualised as follows:

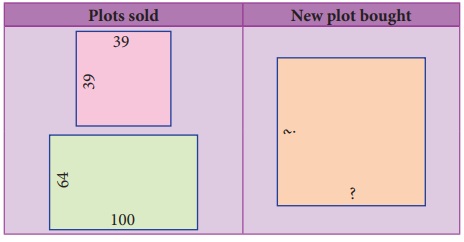
Area of the square plot bought = [ Area of the square plot sold ] + [ Area of the rectangular plot sold ]

= [ 39×39 ] + [ 100 × 64 ]

= [ 1521 ] + [ 6400 ]

= 7921 m²

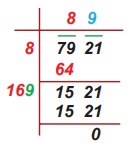
Length of a side of the new square plot = √7921 = 89 m