Exercise 1.3 (Properties of Rational Numbers)

Exercise 1.3

1. Verify the closure property for addition and multiplication for the rational numbers −5/7 and 8/9 .

Solution:

Closure property for addition.

Let a = −5/7  and b = 8/9 be the given rational numbers.

a + b = −5/7 + 8/9

= [ (−5 × 9) + (8 × 7)] / [7 × 9]

= [−45 + 56] / 63 = 11 / 63  is in Q.

i.e a + b = [−5/7] + [8/9] = 11/63  is in Q.

∴ Closure property is true for addition of rational numbers.

Closure property for multiplication

Let  a = −5/7 and b = 8/9

a × b = −5/7 × 8/9 = −40/63 is in Q.

∴ Closure property is true for multiplication of rational numbers. 

2. Verify the commutative property for addition and multiplication for the rational numbers −10/11 and −8/33

Solution:

Let a = −10/11 and b = −8/33 be the given rational numbers.

Now a + b = −10/11 + (−8/33) = [ (−10 × 3) + (−8 × 1)] / 33 = [−30 + (−8)] / 33

a + b = −38/33        ………….(1)  

b + a =  (−8/33) + (−10/11) = [ (−8 × 1) + ((−10) × 3)] / 33   = [−8 + (−30)] / 33

b + a =  − 38 / 33 …………..(2)

From (1) and (2)

a + b = b + a and hence addition is commutative for rational numbers.

Further a × b = −10/11 × (−8/33) = 80/363

a × b = 80/363  …………….(3)

b × a = −8/33 × (−10/11) = 80/363

b × a = 80/363 ………….(4)

From (3) and (4) a × b = b × a

Hence multiplication is commutative for rational numbers.

3. Verify the associative property for addition and multiplication for the rational numbers −7/9 , 5/6 and −4/3.

Solution:

Let a = −7/9, b = 5/6,  c = −4/3 be the given rational numbers.

(a + b) + c = (−7/9 + 5/6) + (−4/3) = ( [−7 × 2 + 5 × 3] / 18 ) + (−4/3)

= ( [−14 + 15] / 18) + (−4/3) = 1/18 + (−4/3)

= [1 + (−4) × 6] / 18 = [ 1 + (−24) ] / 18 = −23/18 ……..(1)

a + (b + c ) = −7/9 + (5/6 + (−4)/3) = −7/9 + ( [5 + (−4) 2] / 6) 

= −7/9 + ( [5 + (−8)] / 6) = −7/9 + (−3/6) = −7/9 + (−1/2)

= [−7 × 2 + (−1) × 9] / 18 = [ −14 + (−9) ] / 18 = −23/18 ……..(2)

From (1) and (2), (a + b) + c = a + (b + c) is true for rational numbers.

Now

(a × b) × c = (−7/9 × 5/6) × (−4/3) = ( [−7 × 5] / [9 × 6] ) × (−4/3)

= −35/54 × −4/3 = [−35 × (−4)] / [54 × 3] = 70/81 ………(1)

a × (b x c) = −7/9 × ([5/6] × [−4/3]) = −7/9 ×  [5 × (−2)] / [3 × 3]

= −7/9 × (−10)/9  = 70/81 ………(2)

From (1) and (2) (a × b) × c = a × (b × c) is true for addition and multiplication for the rational numbers.

Thus associative property.

4. Verify the distributive property a × (b + c ) = ( a × b ) + ( a + c) for the rational numbers a = -1/2 , b = 2/3 and c = -5/6 .

Solution:

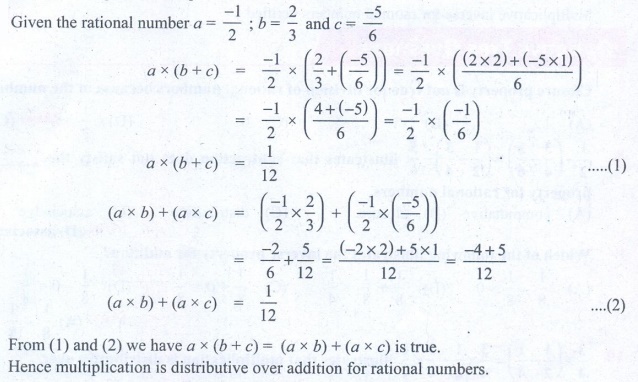
Given the rational number a = −1/2 ; b = 2/3 and c = −5/6

a × (b + c) = −1/2 × (2/3 + (−5/6)) = −1/2 × ( [(2 × 2) + (−5 × 1)] /6 )

= −1/2 × ( [4 + (−5)] / 6 ) = −1/2 × (−1/6)

a × (b + c) = 1/12 ………(1)

 (a × b) + (a × c) = (−1/2 × 2/3) + ( −1/2 × (−5/6) )

= −2/6 + 5/12 = [(−2 × 2) + 5 × 1] / 12 = [−4 + 5] / 12

(a × b) + (a × c) = 1/12   ………(2)

From (1) and (2) we have a × (b + c)  = (a × b) + (a × c) is true.

Hence multiplication is distributive over addition for rational numbers.

5. Verify the identity property for addition and multiplication for the rational numbers 15/19 and −18/25.

Solution:

[15/19] + 0 = [15/19] + [0/19] = [15 + 0] / 19 = 15/19

[−18/25] + 0 = [−18/25] + [0/25] = [−18 + 0] / 25 = −18/25

Identify property for addition verified.

[15/19] × 1 = [15 × 1] / 19 = 15/19

[−18/25] × 1 = [−18 × 1] / 25 = −18/25

Identify property for multiplication verified.

6. Verify the additive and multiplicative inverse property for the rational numbers −7/17 and 17/27.

Solution:

−7/17 + 7/17 = [−7 + 7] / 17 = 0/17 = 0

17/27 + (−17/27) = [17 + (−17)] / 27 = 0/27 = 0

Additive inverse for rational numbers verified.

−7/17 × 17/−7 = [−7 × 17] / [17 × (−7)] = 1

17/27 × 27/17 = [17 × 27] / [27 × 17] = 1

Multiplicative inverse for rational numbers verified.

Objective Type Questions

7. Closure property is not true for division of rational numbers because of the number

(A) 1

(B) –1

(C) 0

(D) 1/2

[Answer: (C) 0 ]

8. 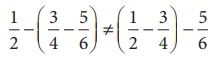 illustrates that subtraction does not satisfy the ________ property for rational numbers.

(A) commutative

(B) closure

(C) distributive

(D) associative

[Answer: (D) associative]

9. Which of the following illustrates the inverse property for addition?

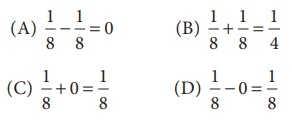
[Answer: (A) 1/8 – 1/8 = 0]

10. 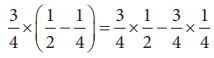 illustrates that multiplication is distributive over

(A) addition

(B) subtraction

(C) multiplication

(D) division

[Answer: (B) subtraction]

We know that different operations with the same pair of rational numbers usually give different answers. Check the following calculations which are some interesting exceptions in rational numbers.

(i) 13/4 + 13/9 = 13/4 × 13/9

(ii) 169/30 + 13/15 = 169/30 ÷ 13/15

Amazing …! Isn’t it? Try a few more like these, if possible.

Think

Observe that, 

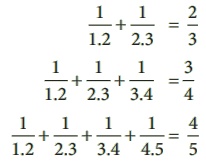
Use your reasoning skills, to find the sum of the first 7 numbers in the pattern given above.

Solution:

1/1.2 + 1/2.3 + 1/3.4 + 1/4.5 + 1/5.6 + 1/ 6.7 + 1/7.8 = 7 / 8

Answer:

Exercise 1.3

Verify yourself for Qns 1 to 6.

7. (C) 0

8. (D) associative

9. (A) 1/8 – 1/8 = 0

10. (B) subtraction