Decimal representation of a rational number

Decimal representation of a rational number

A rational number can be nicely represented in decimal form rather than in the usual fractional form. Given a rational number in the form a/b (b ≠ 0), just divide the numerator a by the denominator b and we can see that it can be expressed as a terminating or non-terminating, recurring decimal.

Activity

Use a string as a number line and fix it on the wall, for the length of the class room. Just mark the integers spaciously and ask the students to pick the rational number cards from a box and fix it roughly at the right place on the number line string. This can be played between teams and the team which fixes more number of cards correctly (by marking) will be the winner.

Example 1.1

Write the decimal forms of the following rational numbers:

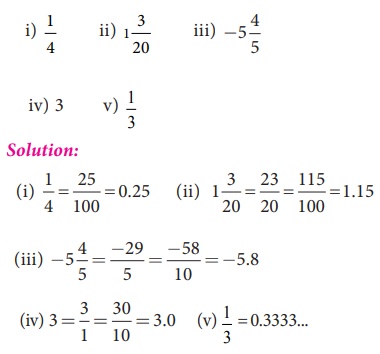
(by actual division and it is recurring and non-terminating)

Note

The above examples show how a rational number may be given in decimal form. The reverse process of converting the decimal form of a rational number to the fractional form may be seen in the higher classes.

There are decimal numbers which are non-terminating and non-recurring such as

π = 3.141592653589793238462643…..

√2 = 1.41421356237309504880168……. etc.

They are not rational numbers and one can study more about them in the higher classes.

Try these

Write the decimal forms of the following rational numbers:

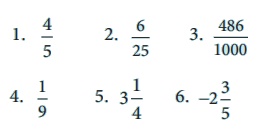
Solution:

1. 4/5 = [4 × 20] / [5 × 20] = 80 / 100 = 0.80

2. 6/25 = [6 × 4] / [25 × 4] = 24 / 10 = 0.24

3. 486/1000 = 0.486