Exponents and Powers

Exponents and Powers

We know how to express some numbers as squares and cubes. For example, we write 5² for 25 and 5³ for 125.

In general terms, an expression that represents repeated multiplication of the same factor is called a power. The number 5 is called the base and the number 2 is called the exponent (more often called as power). The exponent corresponds to the number of times the base is used as a factor.

1. Powers with positive exponents

Value of powers given by positive whole number exponents quite often increase rapidly.

Observe the following example:

2¹ =2

2² = 2×2=4

2³ = 2×2×2=8

2⁴ = 2×2×2×2 =16

2⁵ = 2×2×2×2×2=32

2⁶ = 2×2×2×2×2×2=64

2⁷ = 2×2×2×2×2×2×2=128

2⁸ = 2×2×2×2×2×2×2×2=256

2⁹ = 2×2×2×2×2×2×2×2×2=512

2¹⁰ = 2×2×2×2×2×2×2×2×2×2=1024

At this rate of increase, what do you think 2¹⁰⁰ will be?

In fact, 2¹⁰⁰=1267650600228229401496703205376

Thus, we understand that the positive exponential notation with positive power could be useful when we come across with large numbers.

2. Powers with zero and negative exponents

Observe this pattern:

2⁵= 32

2⁴= 16

2³= 8

2²= 4

2¹= 2

2⁰=?

Starting from the beginning, what happens in the successive steps? We find that the result is half of that of the previous step. So, what can we say about 2⁰ ? If we prepare a table like this for 3⁵, 3⁴, 3³, and so on what will it tell us about 3⁰? We can use the same process as in this pattern, to conclude that any non-zero number raised to the zero exponent must result in 1. Thus,

 a⁰ = 1, where a ≠ 0

Let us see what happens if we extend the above pattern further downward.

As before, starting from the beginning, in the successive steps, we find that the result is half of that of the previous step. Since 2⁰ = 1, the next step is 2^–1, whose value is the previous step’s value 1, divided by 2, that is 1/2 . Next is 2^–2, which is the same as 1/2 divided by 2, that is 1/4 and so on. Thus,

2³  = 8

2²  = 4

2¹  = 2

2⁰  = 1

2^–1 = 1/2

2^–2 = 1/4

2^–3 = 1/8

In general, a^−m = 1/a^m , where m is an integer

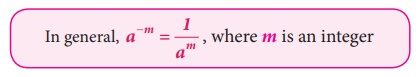
3. Expanded form of numbers using exponents

In the lower classes, we have learnt how to write a whole number in the expanded form. For example, 5832 = 5×1000 + 8×100 + 3×10 + 2×1

= 5×10³ + 8×10² + 3×10¹ + 2 (when we use exponential notation).

What shall we do if we get decimal places? Powers of 10 with negative exponents come to our rescue!

Thus, 58.32 = 50 + 8 + 3/10 + 2/100

= 5×10 + 8×1 + 3× (1/10) + 2 × (1/100)

= 5×10¹ + 8×10⁰ + 3×10^–1 + 2×10^–2

Try these

Expand the following numbers using exponents:

1.8120 2. 20305 3. 3652.01 4. 9426.521

Solution:

(i) 8120 = (8 × 1000) + (1 × 100) + (2 × 10) + 0 × l

 = (8 × 10³) + (1 × 10²) + (2 × 10¹)

(2) 20305 = (2 × 10000) + (0 × 1000) + (3 × 100) + ( 0 × 10) + (5 × 1)

 = (2 × 10⁴) + (3 × 10²) + 5 

(3) 3652.01 = 3000 + 600 + 50 + 2 + 0/10 + 1/100

= (3 × 1000) + (6 × 100) + (5 × 10) + (2 × 1) + 1 × 1/100)

 = (3 × 10³) + (6 × 10²) + (5 × 10¹) + 2 + (1 × 10⁻²)

(4) 9426.521 = (9 × 1000) + (4 × 100) + (2 × 10) + (6 × 1) + (5/10) + (2/100) + (1/1000)

= (9 × 10³) + (4 × 10²) + (2 × 10¹) + 6 + (5 × 10⁻¹) + (2 × 10⁻²) + (1 × 10⁻³)

4. Laws of Exponents

Laws of exponents arise out of certain basic ideas. A positive exponent of a number indicate how many times we use that number in a multiplication whereas a negative exponent suggests us how many times we use that number in a division, since the opposite of multiplying is dividing.

• Product law

According to this law, when multiplying two powers that have the same base, we can add the exponents. That is,

a^m × aⁿ = a^{m + n}

where a (a≠0), m, n are integers. Note that the base should be the same in both the quantities.

Examples:

• Quotient law

According to this law, when dividing two powers that have the same base we can subtract the exponents. That is,

a^m / aⁿ = a^m-n

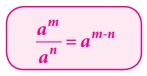
where a (a ≠ 0), m, n are integers. Note that the base should be the same in both the quantities.

How does it work? Study the following examples.

Examples:

• Power law

According to this law, when raising a power to another power, we can just multiply the exponents.

(a^m)ⁿ = a^mn

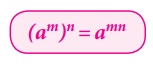
where a (a ≠ 0), m, n are integers.

Examples:

[(- 2)³ ]² = (- 2)^3×2 by law and (-2)⁶ = 64

[(-2)³]² = [(-2)× (-2)× (-2)]² = [-8]² = 64

Try these

Verify the following rules (as we did above). Here, a,b are non-zero integers and m, n are any integers.

1. Product of same powers to power of product rule: a ^m × b ^m = (ab)^m

2. Quotient of same powers to power of quotient rule: aⁿ/b^m = (a/b) ^m

3. Zero exponent rule: a⁰ = 1.

Verification:

Let a = 2; b = 3; m = 2

1. a^m × b^m = 2² × 3² = 4 × 9 = 36 = (2 × 3)²

2. a^m / b^m = 2² / 3² = 4 / 9 = (2 / 3)²

3. a⁰ = 2⁰ = 1.

Example 1.36

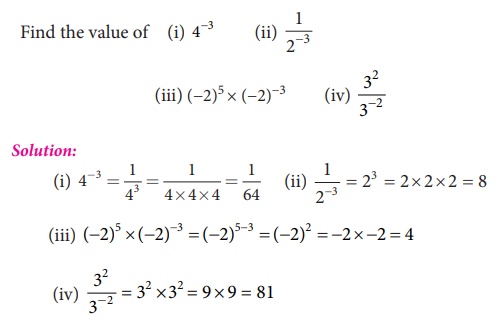
Example 1.37

Simplify and write the answer in exponential form:

(i) (3⁵ ÷ 3⁸)⁵ × 3^–5 (ii) ( −3)⁴ × (5/3)⁴

Solution:

 (i) (3⁵ / 3⁸)⁵ × 3^–5 = (3^5-8) × 3^-5 = (3^-3)⁵ × 3^-5 = 3^-3×5 = 3^-3×5 = 3^-15 × 3^-5 = 3^-15-5 = 3^-20

 (ii) (-3)⁴ × (5/3)⁴ = 3⁴ × 5⁴/3⁴ = 5⁴

Example 1.38

Find x so that ( −7 ) ^x+2 × ( −7 )⁵ = ( −7)¹⁰

Solution:

(-7 )^x+2 × (-7)⁵ = (-7)¹⁰

(-7) ^x+2+5 = (7)¹⁰

Since the bases are equal, we equate the exponents to get

 x + 7 = 10

 x =10 - 7 = 3

5. Standard Form and Scientific Notation

Standard form of a number is just the number as we normally write it. We use expanded notation to show the value of each digit. That is, it is exhibited as a sum of each digit duly multiplied by its matching place value (like ones, tens, hundreds etc.,). For example, 195 is in standard form. It can be expanded as 195 = 1 × 100 + 9 × 10 + 5 × 1.

Astronomers, biologists, engineers, physicists and many others come across quantities whose measures require very small or very large numbers. If they write the numbers in standard form, it may not help us to understand or make computations easily. Scientific notation is a way to make these numbers easier to work with.

To write in scientific notation, follow the form S × 10^a. where S is a number (integer or integer with decimal) between 1 and 10, but not 10 itself, and a is a positive or negative integer. Thus, a number in scientific notation is written as the product of a number (integer or integer with decimal) and a power of 10. We move the decimal place forward or backward until we have a number from 1 to 9. Then, we add a power of ten that tells how many places you moved the decimal forward or backward.

Examples:

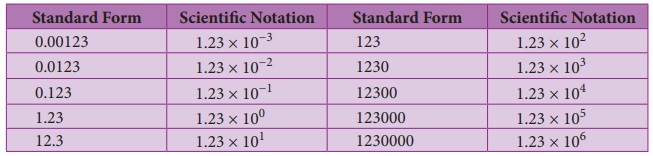
Some more examples:

(a) The diameter of the earth is 12756000 miles. This can be easily written in scientific form as 1.2756×10⁷ miles.

(b) The volume of Jupiter is about 143300000000000 km^3. This can be easily written in scientific form as 1.433×10¹⁴ km³.

(c) The size of a bacterium is 0.00000085 mm. This can be easily written in scientific form as 8.5 ×10⁻⁷ mm

Note

1. The positive exponent in 1.3 ×10¹² indicates that it is a large number.

2. The negative exponent in 7.89 × 10^–21 indicates that it is a small number.

Example 1.39

Combine the scientific notations: (i) (7 × 10²)(5.2 × 10⁷) (ii) (3.7 × 10^-5)(2 × 10^-3)

Solution:

(i) (7 × 10²)(5.2 × 10⁷) = 36.4 × 10⁹ = 3.64 × 10¹⁰

(ii) (3.7 × 10^-5) (2 × 10^-3) =7.4×10^–8

Example 1.40

Write the following scientific notations in standard form:

(i) 2.27 × 10^-4 (ii) Light travels at 1.86 ×10⁵ miles per second.

Solution:

(i) 2.27 × 10^-4 = 0.000227.

(ii) Light travels at 1.86 ×10⁵ miles per second = 186000 miles per second

Try these

1. Write in standard form: Mass of planet Uranus is 8.68 × 10²⁵ kg.

Solution:

Mass of Planet Uranus = 86800000000000000000000000 kg

2. Write in scientific notation: (i) 0.000012005 (ii) 4312.345 (iii) 0.10524 (iv)The distance between the Sun and the planet Saturn 1.4335×10¹² miles.

Solution:

(i)  0.000012005 = 1.2005 × 10⁻⁵

(ii) 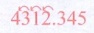 4312.345 = 4.312345 × 10³

(iii) 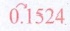 0.l 524 = 1.0524 × 10⁻¹

(iv) The distance between Sun and the planet Saturn is 1.4335 × 10¹² miles