Exercise 1.2: Basic Arithmetic Operations on Rational Numbers

Exercise 1.2

Fill in the blanks:

(i) The value of 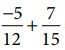 = ________.  [Answer: 1/20 ]

(ii) The value of 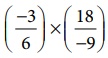 is ________. [Answer: 1 ]

(iii) The value of 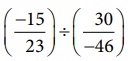 is ________. [Answer: 1 ]

(iv) The rational number ________ does not have a reciprocal.  [Answer: 0 ]

(v) The multiplicative inverse of –1 is ________. [Answer: −1 ]

2. Say True or False:

(i) All rational numbers have an additive inverse. [Answer: True ]

(ii) The rational numbers that are equal to their additive inverses are 0 and –1. [Answer: False ]

(iii) The additive inverse of −11/−17 is 11/17. [Answer: False ]

(iv) The rational number which is its own reciprocal is –1. [Answer: True ]

(v) The multiplicative inverse exists for all rational numbers. [Answer: False ]

3. Find the sum:

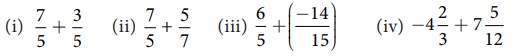
Solution:

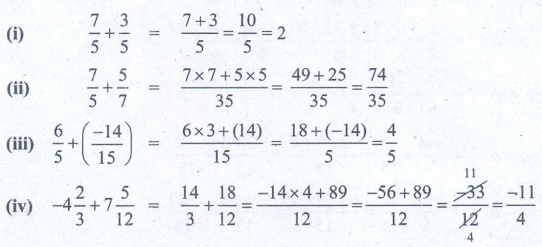
(i) 7/5  + 3/5 = [7+3] / 5 = 10/5 = 2

(ii) 7/5  + 5/7 = [ 7×7 + 5×5] / 35 = [49 + 25] / 35 = 74/35

(iii) 6/5  + (−14/15) = [ 6×3 + (14)] / 15 = [18 + (−14)] / 5 = 4/5

(iv) −4 (2/3)  + 7 (5/12) = [14/3] + [18/12] = [−14 × 4 + 89] / 12 = [−56 +89] / 12 = −33/12 = −11/4

4. Subtract :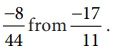 

Solution:

−17/11 – (−8/44) = [−17/11] + [8/44] = [−17 × 4 + 8] / 44 = [−68 + 8] / 44 = 60/44 = −15 / 11

5. Evaluate : 

Solution:

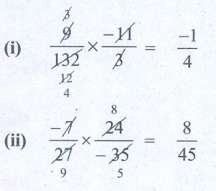
(i) [9 / 132] × [−11 / 3] =  −1 / 4

 (ii) [−7 / 27] × [24 / −35] = 8/45

6. Divide : 

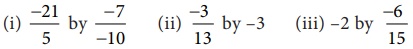
Solution:

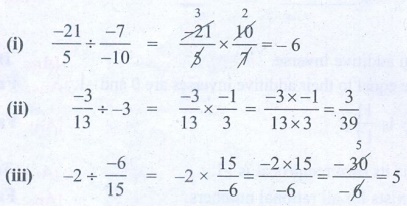
(i) −21/5 ÷ −7/−10 = −21/5 × 10/7 = −6

(ii) −3/13 ÷ −3 =  −3/13 × −1/3 = [−3 × −1] / [13 × 3] = 3/39

(iii) −2 ÷ [−6/15] = −2 × [15/−6] = [−2 × 15] / −6 =  −30 / −6 = 5

7. Find (a + b) ÷ (a - b) if

(i) a = 1/2 , b = 2/3 (ii) a = - 3/5 , b = 2/15

Solution:

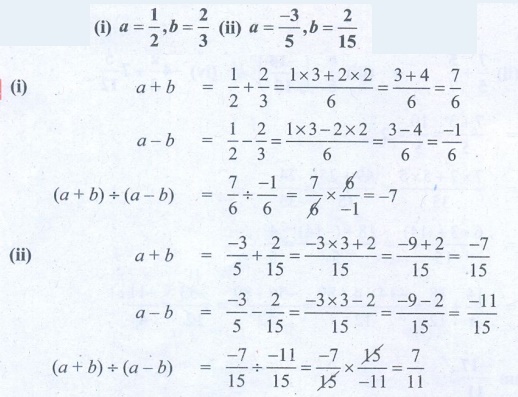
(i) a = 1/2, b = 2/3

 a + b = [1/2]  + [2/3] = [1×3 + 2×2] / 6 = [3 + 4] / 6 = 7/6

a – b = (1/2)  − (2/3) = [1×3 − 2×2] / 6 = [3 – 4] / 6 = −1/6

(a + b) ÷ (a − b) = [7/6] ÷ [−1/6] = [7/6] × [6/−1] = −7

(ii) a = −3/5, b = 2/15

a + b = −3/5 + 2/15 = [ −3×3 + 2] / 15 = [−9 + 2] / 15 = −7/15

a − b = (−3/5) – (2/15) = [−3 × 3 – 2] / 15 = [−9 – 2] / 15 = −11/15

(a + b) ÷ (a − b) = [−7/15] ÷ [−11/15] = [−7/15] × [15/−11] = 7/11

8. Simplify : 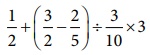 and show that it is a rational number between 11 and 12.

Solution:

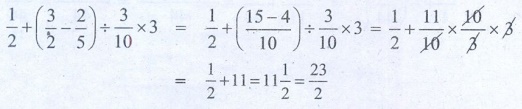
(1/2) + (3/2 – 2/5) ÷  (3/10) × 3 = 1/2 + ([15 – 4] / 10 ) ÷  3/10 × 3 = 1/2 + 11/10 × 10/3 × 3

= 1/2 + 11 = 11 (1/2) = 23/2

9. Simplify :

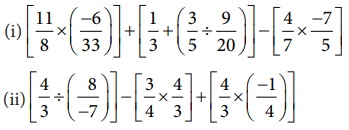
Solution:

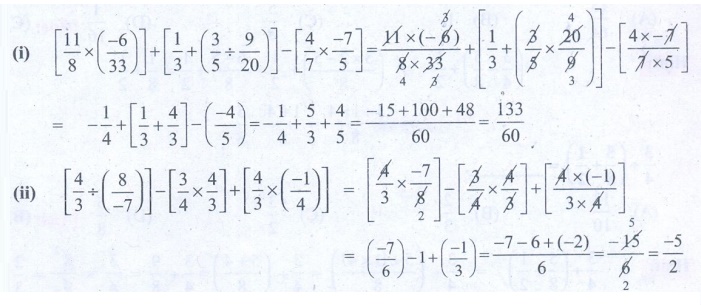
10. A student had multiplied a number by 4/3 instead of dividing it by 4/3 and got than the correct answer. Find the number.

Solution:

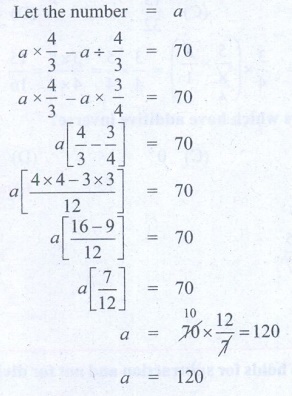
Let the number = a

[ a × 4/3 ] – [ a ÷ 4/3 ] = 70

[ a × 4/3 ] – [ a × 3/4 ] = 70

a [4/3 – 3/4] = 70

a [ (4×4 – 3×3) / 12] = 70

a [ 16–9 / 12] = 70

a [7 / 12] = 70

a  = 70 × (12/7) = 120

 a  = 120

Objective Type Questions

11. The standard form of 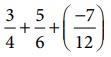 sum is _________

[Answer: (A) 1]

Solution:

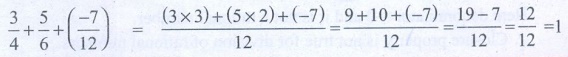
3/4 + 5/6 + (−7/12) = [ (3 × 3) + (5 × 2) + (−7) ] / 12 = [ 9 + 10 + (−7) ] / 12 =  [19 – 7 ] / 12 = 12 / 12 = 1

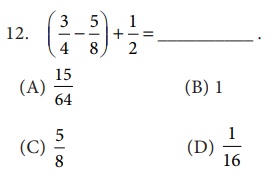
[Answer: (C) 5/8 ]

Solution:

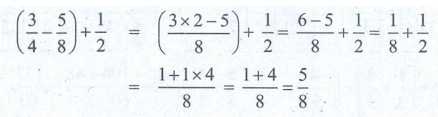
(3/4 – 5/8) + 1/2 = ( [3 × 2 – 5] / 8) + 1/2 = [6 – 5] / 8 + 1/2 = 1/8 + 1/2

= [1 + 1 × 4] / 8 = [1 + 4] / 8 = 5/8

[Answer: (B) 2/3]

Solution:

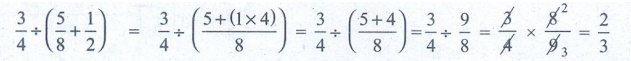
3/4 ÷ (5/8 + 1/2) = 3/4 ÷ ( [5 ÷ (1 × 4)] / 8 ) = 3/4 ÷ ([5+4]/8) = 3/4 ÷ 9/8 = [3/4] × [8/9] = 2/3

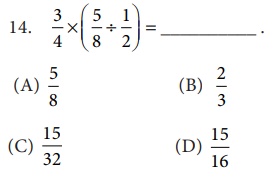
[Answer: (D) 15/16]

Solution:

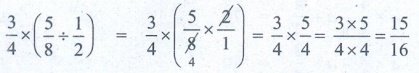
3/4 × ( 5/8 ÷ 1/2) = 3/4 × (5/8 × 2/1) = 3/4 × 5/4 = 3×5 / 4×4 = 15/16

15. Which of these rational numbers which have additive inverse?

(A) 7

(B) −5/7

(C) 0

(D) all of these

[Answer: (D) all of these]

Solution:

Additive inverse of 7 is −7.

Additive inverse of −5/7 is 5/7.

Additive inverse of 0 is 0.

Answer: Exercise 1.2

1. (i) 1/20 (ii) 1 (iii) 1 (iv) 0 (v) –1

2. (i) True (ii) False (iii) False (iv) True (v) False

3. (i) 2 (ii) 74/35 (iii) 4/15 (iv) 2 3/4

4. −15/11

5. (i) −1/4 (ii) 8/45

6. (i) − 6 (ii) 1/13 (iii) 5

7. (i) –7 (ii) 7/11

8. 23/2 (≈11 1/2) and hence lies between 11 and 12.

9. (i) 133/60 (ii) −5/2

10. 120

11. (A) 1

12. (C) 5/8

13. (B) 2/3

14. (D) 15/16

15. (D) all of these