Exercise 1.5 (Cubes and Cube Roots)

Exercise 1.5

1. Fill in the blanks:

(i) The ones digits in the cube of 73 is____________. [Answer: 7]

(ii) The maximum number of digits in the cube of a two digit number is ____________. [Answer: 6]

(iii) The smallest number to be added to 3333 to make it a perfect cube is ___________. [Answer: 42]

(iv) The cube root of 540×50 is ___________. [Answer: 30]

(v) The cube root of 0.000004913 is ___________. [Answer: 0.017]

2. Say True or False:

(i) The cube of 24 ends with the digit 4. [Ans. True]

(ii) Subtracting 103 from 1729 gives 93. [Ans. True]

(iii) The cube of 0.0012 is 0.000001728. [Ans. False]

(iv) 79570 is not a perfect cube. [Ans. True]

(v) The cube root of 250047 is 63. [Ans. True]

3. Show that 1944 is not a perfect cube.

Solution:

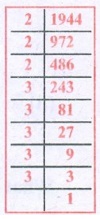
1994 = 2 × 2 × 2 × 3 × 3 × 3 × 3 × 3

        = 2 × 2 × 2 × 3 × 3 × 3 × 3 × 3

        = 23 × 33 × 3 × 3

There are two triplets to make further triplets we need one more 3.

∴ 1944 is not a perfect cube.

4. Find the smallest number by which 10985 should be divided so that the quotient is a perfect cube.

Solution:

We have 10985 = 5 × 13 × 13 × 13

= 5 × 13 × 13 × 13

Here we have a triplet of 13 and we are left over with 5.

If we divide 10985 by 5. the new number will be a perfect cube.

∴ The required number is 5.

5. Find the smallest number by which 200 should be multiplied to make it a perfect cube.

Solution:

We find 200 = 2 × 2 × 2 × 5 × 5

Grouping the prime factors of 200 as triplets, we are left with 5 × 5

We need one more 5 to make it a perfect cube.

So to make 200 a perfect cube multiply both sides by 5.

200 × 5 = (2 × 2 × 2 × 5 × 5) × 5

1000 = 2 × 2 × 2 × 5 × 5 × 5

Now 1000 is a perfect cube.

∴ The required number is 5.

6. Find the cube root of 24 × 36 × 80 × 25.

Solution:

7. Find the cube root of 729 and 6859 by prime factorisation.

Solution:

8. What is the square root of cube root of 46656?

Solution:

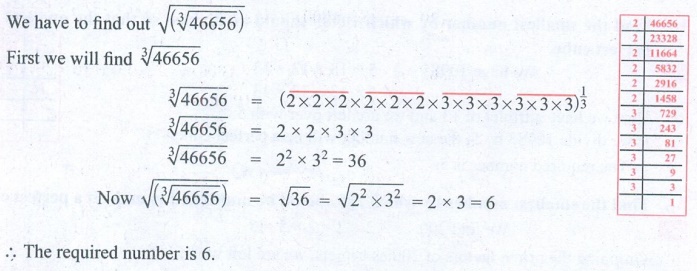
9. If the cube of a squared number is 729, find the square root of that number.

Solution:

We have to find out √3 , √3 = 1.732 

10. Find the two smallest perfect square numbers which when multiplied together gives a perfect cube number.

Solution:

 Consider the numbers 22 and 42

The numbers are 4 and 16.

Their product 4 × 16 = 64

64 = 4 × 4 × 4

∴ The required square numbers are 4 and 16

Activity

Observe that

 23−13=1+2×1×3

 33−23=1+3×2×3

 43−33=1+4×3×3

Find the value of 153 −143 in the above pattern.

Observe that

 13=1=1

 23=8=3+5

 33=27=7+9+11

Continue this pattern to find the value of 73 as the sum of consecutive odd numbers

Answer:

Exercise 1.5

1. (i) 7 (ii) 6 (iii) 42 (iv) 30 (v) 0.017

2. (i) True (ii) True (iii) False (iv) True (v) True

4. 5

5. 5

6. 120

7. 9,19

8. √36 = 6

9. √3 = 1.732

10. 4,16